进度记录

  • 已看完：

    • 基础算法（一）（二）
    • 数据结构（一）（二）
    • 动态规划（一）

  • 在看：

    搜索与图论（一）

    数据结构（三）——STL应用

    动态规划（二）

1.基础算法

排序

  • 快排不稳定，归并稳定

  • 要想使快排稳定，可以把每个值扩展成带下标的二元组，这样就不会出现相同的值

  • 快排平均时间复杂度nlogn，最高可达n^2。归并时间复杂度nlogn。

快速排序——分治

基本流程：

假设区间左端点为l，右端点为r

  • 确定分界点x：分界点选择较为灵活，尽量取q[l + r >> 1]

    分界点：快排取的是数组里的值，归并取的是下标的中值

  • 调整区间：小于等于x的放左边，大于等于x的放右边

  • 递归处理左右两段

几种方法：

暴力法：开两个数组，小的放第一个，大的放第二个，最后再放回最初的数组。

时间复杂度同样O(n)，耗费空间

优雅法：两个指针i和j，i从左端向右端遍历，遇到大于或等于x的数就停下。

j从右端向左端遍历，遇到小于或等于x的数就停下。

两个指针都停下来后交换两处的值。指针相遇时结束。

代码模板：

【经检验】这个模板没问题，但是记得要带上最后对自身的递归调用！

  • 取的pivot必须是中间的值q[l + r >> 1]，不能是q[l]或q[r]
  • 最后记得要带上最后对自身的递归调用
1
2
3
4
5
6
7
8
9
10
11
12
13
void quick_sort(int q[], int l, int r)
{
    if (l >= r) return;

    int i = l - 1, j = r + 1, x = q[l + r >> 1];
    while (i < j)
    {
        do i ++ ; while (q[i] < x);
        do j -- ; while (q[j] > x);
        if (i < j) swap(q[i], q[j]);
    }
    quick_sort(q, l, j), quick_sort(q, j + 1, r);
}

  • partition划分函数的写法

    （力扣例题：**215. 数组中的第K个最大元素**）

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    int partition(vector<int>& q, int l, int r)  //划分函数
    {
        if (l >= r) return r;
        int i = l - 1, j = r + 1, x = q[l + r >> 1];
        while (i < j)
        {
            do i ++ ; while (q[i] < x);
            do j -- ; while (q[j] > x);
            if (i < j) swap(q[i], q[j]);
        }
        partition(q, l, j), partition(q, j + 1, r);
        return i;
    }

    返回的即为一次划分得到的元素的正确位置（return i;和return j;等价）

归并排序——分治

基本流程：

默认均分，先均分再排序，后归并

  • 确定分界点：mid=（l+r）/2
  • 递归排left和right
  • 归并——合二为一

代码模板：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
void merge_sort(int q[], int l, int r)
{
    if (l >= r) return;

    int mid = l + r >> 1;
    merge_sort(q, l, mid);
    merge_sort(q, mid + 1, r);

    int k = 0, i = l, j = mid + 1;
    while (i <= mid && j <= r)
        if (q[i] <= q[j]) tmp[k ++ ] = q[i ++ ];
        else tmp[k ++ ] = q[j ++ ];

    while (i <= mid) tmp[k ++ ] = q[i ++ ];
    while (j <= r) tmp[k ++ ] = q[j ++ ];

    for (i = l, j = 0; i <= r; i ++, j ++ ) q[i] = tmp[j];
}

例题：

排序的STL写法（用时反而更短）

1
2
3
4
5
6
7
8
9
10
11
12
13
#include <bits/stdc++.h>
using namespace std;
const int N=1e6+10;
int q[N],n;
int main()
{
    scanf("%d",&n);
    for(int i=0;i<n;i++)
        scanf("%d",&q[i]);
    sort(q,q+n);
    for(int i=0;i<n;i++)
        printf("%d ",q[i]);
}

**\788. 逆序对的数量:**这道题细节很多，重复学习 归并排序的应用

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include <bits/stdc++.h>
typedef long long LL;
using namespace std;
const int N=1e6+10;
int q[N],tmp[N],n;

LL merge_sort(int l,int r)
{
    if(l>=r) return 0;

    int mid =l+r>>1;
    LL res =merge_sort(l,mid)+merge_sort(mid+1,r);

    //左右两部分归并的过程
    int k=0,i=l,j=mid+1;
    while(i<=mid&&j<=r)
        if(q[i]<=q[j]) tmp[k++]=q[i++];
        else
        {
            tmp[k++]=q[j++];
            res+=mid-i+1;
        }
    
    //收尾
    while (i<=mid) tmp[k++]=q[i++];
    while (j<=r)   tmp[k++]=q[j++];
    
    //物归原主
    for(int x=l,y=0;x<=r;x++,y++) q[x]=tmp[y];

    return res;
}
int main()
{
    scanf("%d",&n);
    for(int i=0;i<n;i++)
        scanf("%d",&q[i]);
    cout<<merge_sort(0,n-1);
    return 0;
}

解析视频

二分查找

用二分查找元素要求数组的有序性或者拥有类似于有序的性质

整数二分

基本流程：

如果一个区间可以按照某个性质被分为左右两半，一半满足该性质，另一半不满足，则可以使用整数二分来寻找该性质的边界，即左右两半的边界的位置

代码模板：

结合下面的例题理解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
bool check(int x) {/* ... */} // 检查x是否满足某种性质

// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用：（即mid处的数可能为所求的数时）
int bsearch_1(int l, int r)
{
    while (l < r)
    {
        int mid = l + r >> 1;
        if (check(mid)) r = mid;    // check()判断mid是否满足性质
        else l = mid + 1;
    }
    return l;
}
// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用：（即mid处的数不可能为所求的数时）
int bsearch_2(int l, int r)
{
    while (l < r)
    {
        int mid = l + r + 1 >> 1;
        if (check(mid)) l = mid;
        else r = mid - 1;
    }
    return l;
}

模板题：AcWing 789. 数的范围 这道题也要多看 来熟悉整数二分

用于划分的性质1：大于等于x。其左边界为x第一次出现的位置，左边界不用加一

用于划分的性质2：小于等于x。其右边界为x第一次出现的位置，右边界要加一

两个性质来区分左右边界

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include <bits/stdc++.h>
using namespace std;
const int N=1e6+10;
int q[N],n,m,k;
int tmp[2];
int main()
{
    scanf("%d %d",&n,&m);
    for(int i=0;i<n;i++)
        scanf("%d",&q[i]);
    for(int i=0;i<m;i++)
    {
        scanf("%d",&k);
        int l=0,r=n-1;
        while(l<r)//这是求左边界
        {
            int mid=l+r>>1;
            if(q[mid]>=k)
                r=mid;
            else l=mid+1;
        }
        tmp[0]=l;
        l=0,r=n-1;
        while(l<r)//这是求右边界
        {
            int mid=l+r+1>>1;
            if(q[mid]>k)
                r=mid-1;
            else l=mid;
        }
        tmp[1]=l;
        if(q[l]!=k) 
            printf("-1 -1\n");
        else 
            printf("%d %d\n",tmp[0],tmp[1]);
    }
    return 0;
}

浮点数二分

浮点数二分不用考虑边界问题，所以比整数二分简单许多

例题为\790. 数的三次方根

注意上题有很多特殊情况需要考虑，这也是以后做oj题目需要注意的地方

高精度

  • 一般是4种：A+B、A-B、A乘a、A除以b（大写表示该数较大，小写表示该数较小）
  • 大整数用数组存储，相当于用代码模拟加减乘除的过程

高精度加法

代码模板：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// C = A + B, A >= 0, B >= 0
vector<int> add(vector<int> &A, vector<int> &B)
{
    if (A.size() < B.size()) return add(B, A);

    vector<int> C;
    int t = 0;
    for (int i = 0; i < A.size(); i ++ )
    {
        t += A[i];
        if (i < B.size()) t += B[i];
        C.push_back(t % 10);
        t /= 10;
    }

    if (t) C.push_back(t);
    return C;
}

模板题 AcWing 791. 高精度加法 总结见提交记录代码注释

高精度减法

  • 需要保证得到的差为正数

    A-B，若A<B，则交换A和B

代码模板：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
// C = A - B, 满足A >= B, A >= 0, B >= 0
vector<int> sub(vector<int> &A, vector<int> &B)
{
    vector<int> C;
    for (int i = 0, t = 0; i < A.size(); i ++ )
    {
        t = A[i] - t;
        if (i < B.size()) t -= B[i];
        C.push_back((t + 10) % 10);
        if (t < 0) t = 1;
        else t = 0;
    }

    while (C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}

模板题 AcWing 792. 高精度减法 总结见该题代码注释

该题要注意：

  • 要先比较两数大小，确保减数大于被减数，最后再分情况处理

  • 注意前导0问题的处理

最终整数范围内的所有加减运算问题都可以转换成|A|+|B|或|A|-|B|问题

高精度乘法

  • C=A*b

代码模板：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
// C = A * b, A >= 0, b >= 0
vector<int> mul(vector<int> &A, int b)
{
    vector<int> C;

    int t = 0;
    for (int i = 0; i < A.size() || t; i ++ )
    {
        if (i < A.size()) t += A[i] * b;
        C.push_back(t % 10);
        t /= 10;
    }

    while (C.size() > 1 && C.back() == 0) C.pop_back();

    return C;
}

要注意的是：此处计算乘法的思路与手算不同，使用t+=A[i]*b来计算

边界条件是乘以0

模板题：AcWing 793. 高精度乘法

高精度除法

  • A / b = C … r, A >= 0, b > 0

代码模板：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
// A / b = C ... r, A >= 0, b > 0 ，高精度除以低精度
vector<int> div(vector<int> &A, int b, int &r)
{
    vector<int> C;
    r = 0;
    for (int i = A.size() - 1; i >= 0; i -- )
    {
        r = r * 10 + A[i];
        C.push_back(r / b);
        r %= b;
    }
    reverse(C.begin(), C.end());//reverse()函数
    while (C.size() > 1 && C.back() == 0) 
        C.pop_back();//取出前导0
    return C;
}

reverse()函数 #include <algorithm>

pop_back()函数 #include <vector>

vector去掉首个元素：

vector<int>::iterator k = v.begin();

v.erase(k);

模板题：AcWing 794. 高精度除法

前缀和与差分

一维前缀和

  • Si=数组中前i项的和
  • 作用：可以用于计算某段数字的和，且复杂度较低
  • 注意要定义S0为0，方便边界情况计算

思路模板：

S[i] = a[1] + a[2] + ... a[i]

a[l] + ... + a[r] = S[r] - S[l - 1]

注意！！！一般来讲s[0]和a[0]都是0，方便边界条件计算，但是具体要看题目要求，最后计算时数组下标也要相应调整！！！

模板题：

AcWing 795. 前缀和

输入输出使用标准输入输出会节省时间 见下图

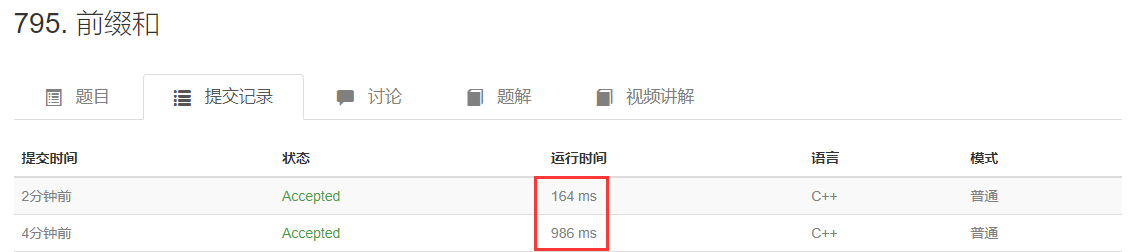
使用scanf/printf输入输出，或使用cin/cout + std::ios_base::sync_with_stdio(false)等对cin/cout进行优化

详见本文

建议数据范围在1e6之内时都可以用cin/cout

二维前缀和

推导过程：

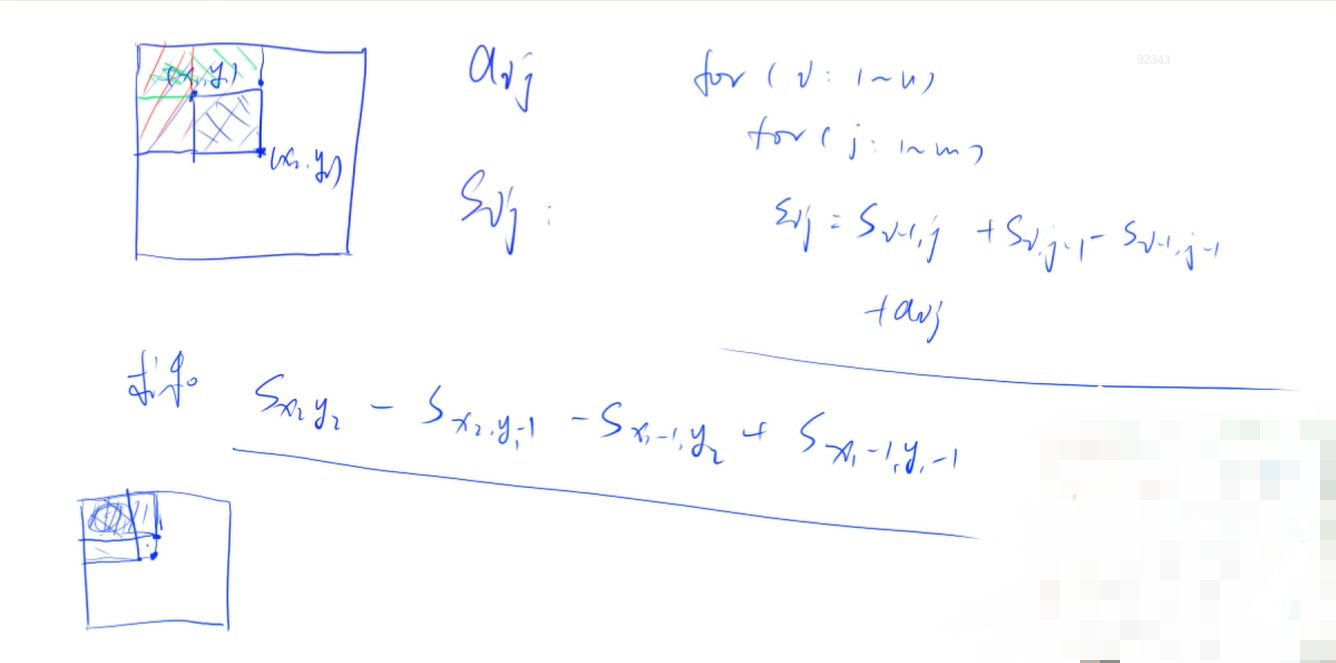
二维前缀和

思路模板：

S[i, j] = 第i行j列格子左上部分所有元素的和

以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵的和为： S[x2, y2] - S[x1 - 1, y2] - S[x2, y1 - 1] + S[x1 - 1, y1 - 1]

！！！注意上述公式中的数组下标！！！

模板题：

AcWing 796. 子矩阵的和

注意！！！一般来讲s[0] [0]和a[0] [0]都是0，方便边界条件计算，但是具体要看题目要求，最后计算时数组下标也要相应调整！！！

相应的读入数据时的细节：for(int i=1;i<=n;i++)

一维差分

差分是前缀和的逆运算

前缀和数组和差分数组相互求的时间复杂度只要O(n)

前缀和数组中某段元素都+c，可以在差分数组中修改两个元素，时间复杂度为O(1)

797. 差分

二维差分

与一维思想类似，是二维前缀和的逆运算

798. 差分矩阵

这里到第一章的基础算法（二）

2.数据结构

链表

动态链表形式

由于这种基于指针的动态链表的new操作耗时很大，在对时间复杂度有要求的笔试题目中一般不采用这种方式而采用数组构建链表

单链表：常用于邻接表，用于储存树和图

双链表：用于优化某些问题


数组表示链表 图示：

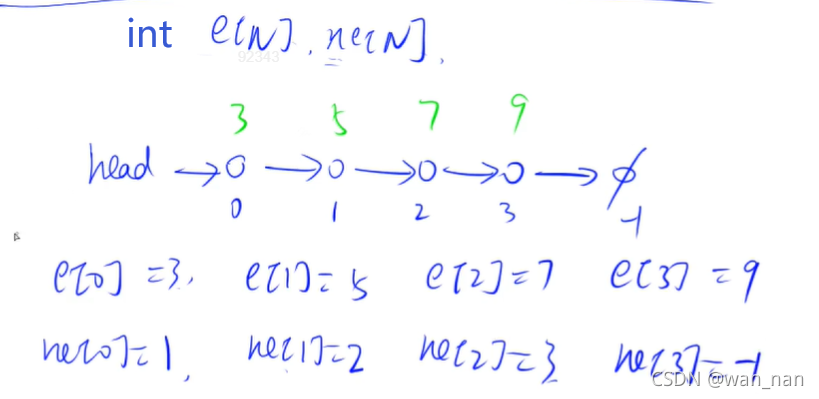
链表数组表示

双链表

与单链表不同的是：

双链表初始化的时候默认存在两个端点，放在idx=0和idx=1处，这样会使相关操作更方便，也可以避免插入操作时的边界问题

1
2
3
4
5
void init()
{
    r[0] = 1, l[1] = 0;
    idx = 2;
}

双链表的相关操作要看看这道题

代码模板：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
// e[]表示节点的值，l[]表示节点的左指针，r[]表示节点的右指针，idx表示当前用到了哪个节点
int e[N], l[N], r[N], idx;

// 初始化——————————————————————初始化的思想比较重要
void init()
{
    //0是左端点，1是右端点
    r[0] = 1, l[1] = 0;
    idx = 2;
}

// 在节点a的右边插入一个数x
void insert(int a, int x)
{
    e[idx] = x;
    l[idx] = a, r[idx] = r[a];
    l[r[a]] = idx, r[a] = idx ++ ;
}

// 删除节点a
void remove(int a)
{
    l[r[a]] = l[a];
    r[l[a]] = r[a];
}

队列和栈

直接用STL

单调栈

确保栈内的数据从栈低到栈顶一直有序

应用如：

  • 【求一个数字序列中 所有数的左/右边 比该数小/大的最近的数】可以从O(n^2)降到O(n)

    题目：给定一个长度为 N的整数数列，输出每个数左边第一个比它小的数，如果不存在则输出 −1

可以看看这篇文章

单调队列

单调队列一般用到的是STL中的双端队列deque

应用如：

  • 【求滑动窗口的 最大值/最小值】（这里发现其实单调栈和单调队列的思想很类似）

    题目：滑动窗口从数组的最左边移动到最右边，求窗口中数字的最大值和最小值

    //贴一下代码

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    #include <iostream>
    #include <cstring>
    #include <algorithm>
    #include <deque>//双端队列deque
    using namespace std;
    const int N = 1e6+10;
    int n,k;
    deque<int> q;
    int a[N];
    int main()
    {
        cin>>n>>k;
        for (int i = 0; i < n; i ++ )
            cin>>a[i];
        //-------------输出最小值-------------//
        for (int i = 0; i < n; i ++ )//队列中存的是下标，不是值
        {
            if(!q.empty()&&i-k+1>q.front())
                q.pop_front();
            while(!q.empty()&&a[q.back()]>=a[i])
                q.pop_back();
            q.push_back(i);
            if(i>=k-1)//在输出之前确保滑动窗口已经涵盖了3个数，而不是1个或者2个
                cout<<a[q.front()]<<' ';
        }
        puts("");
        q.erase(q.begin(),q.end());//   记得清空q    //   “q.”    //  q.front(),q.back()---->q.begin(),q.end()
        //-------------输出最大值-------------//
        for (int i = 0; i < n; i ++ )//队列中存的是下标，不是值
        {
            if(!q.empty()&&i-k+1>q.front())
                q.pop_front();
            while(!q.empty()&&a[q.back()]<=a[i])
                q.pop_back();
            q.push_back(i);
            if(i>=k-1)
                cout<<a[q.front()]<<' ';
        }
    }
    • 双端队列头文件#include <deque>//双端队列deque
    • 队列中保存下标 更方便
    • q.begin(),q.end()返回的是迭代器，而q.front(),q.back()返回的是值

KMP

用string类的find()，时间效率会比手撕KMP差一点点

链接处的此题分别用了KMP和string.find()举例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
//用string.find()的例子
#include<bits/stdc++.h>
using namespace std;
 
int main(void){
	string a,b;
	while(cin>>a){
		getchar();//取消换行对后面的string的影响
		cin>>b;
		int i=0,ans=0;
		while(1){
			i=a.find(b,i);//从i位置开始，寻找第一个出现b的位置 
			if(i==-1)
			break;
			if(i!=-1) ans++;
			i++;
		}
		printf("%d\n",ans);
	}
	return 0;
}

搞清楚KMP，关键是搞清楚next数组的含义

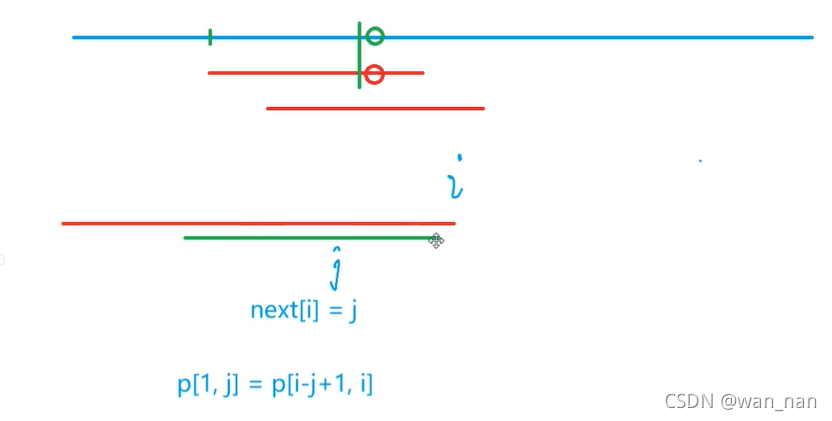KMP-next数组 蓝色串是被比较串，红色串是比较串

next[i]=j //红色串的长度为j的前缀串 与 红色串从下标为i处往前数的长度为j的后缀串 完全相同

也就是说next数组完全由红色串决定


AcWing上的板子边界不好懂，修改如下

下面的例子是借助例题KMP字符串来说明的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
// s[]是长文本，p[]是模式串，n是s的长度，m是p的长度
//求模式串的Next数组：
for (int i = 1, j = 0; i < n; i++)
{
	while (j && p[i] != p[j])
		j = ne[j - 1];
	if (p[i] == p[j])
		j++;
	ne[i] = j;
}

// 匹配
for (int i = 0, j = 0; i < m; i++)
{
	while (j && s[i] != p[j])
		j = ne[j - 1];
	if (s[i] == p[j])
		j++;

	if (j == n)
	{
	    /*匹配成功后的逻辑
		printf("%d ", i - n + 1);
		匹配成功后的逻辑*/
		j = ne[j - 1];
	}
}

参考链接1 参考链接2

Trie树

Trie树，即字典树，又称单词查找树或键树，是一种树形结构，是一种哈希树的变种。典型应用是用于统计和排序大量的字符串（但不仅限于字符串），所以经常被搜索引擎系统用于文本词频统计。它的优点是：最大限度地减少无谓的字符串比较，查询效率比哈希表高。

Trie的核心思想是空间换时间。利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。

1
2
3
4
int son[N][26],cnt[N],idx;//下标为x的点的所有儿子就存在son[x][26]中
//son第一维储存字符的下标，第二维储存26个字母种可能
//cnt储存对应下标字符串出现的次数
//idx与链表的数组存储形式中的idx相似

上述存储方式是trie树实现的精髓

每个点idx唯一

代码实现见835.Trie字符串统计

例题如下：

835.Trie字符串统计

143.最大异或对

问题如果能被转化成数字/大写字母/小写字母的存储查询问题，就可以用Trie树

上述最大异或对问题，就可以把数字转化为01串进行存储，查询一个01串的最大异或对即 查找尽量多的位的相反数

并查集

常考 并查集可以用来维护很多额外信息

例如：（已经出现过的）

(算法题中路径压缩和按秩合并一般只做前者就够了，下面也只做了路径压缩)

并查集主要用于解决一些元素分组的问题。它管理一系列不相交的集合，并支持两种操作：

  • 合并（Union）：把两个不相交的集合合并为一个集合。
  • 查询（Find）：查询两个元素是否在同一个集合中。
并查集

例题 836.合并集合

并查集的精髓在于find()函数，用于查找某个结点的祖宗结点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include <iostream>
using namespace std;
const int N = 1e5+10;

int m,n;
int p[N];//存每个点的父结点

int find(int x)//返回x的祖宗节点，即x属于哪个集合
{
    if(p[x]!=x)
        p[x]=find(p[x]);
    //return x;
    return p[x];//这里必须是p[x] 不能是x
}

int main()
{
    cin>>n>>m;
    for (int i = 1; i <= n; i ++ )
        p[i]=i;//初始化
    while (m -- )
    {
        char c; int a,b;
        cin>>c>>a>>b;
        if(c=='M')
            p[find(a)]=find(b);
        else if(c=='Q')
        {    
            if(find(a)==find(b))
                cout<<"Yes"<<endl;
            else
                cout<<"No"<<endl;
        }
    }
}

例题 837.连通块中点的数量

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include <iostream>
using namespace std;
const int N = 1e5+10;

int m,n;
int p[N];//存每个点的父结点
int nums[N];//所在连通块的点的个数，只保证根节点的nums是有意义的

int find(int x)//返回x的祖宗节点，即x属于哪个集合
{
    if(p[x]!=x)
        p[x]=find(p[x]);
    //return x;
    return p[x];//这里必须是p[x] 不能是x
}

int main()
{
    cin>>n>>m;
    for (int i = 1; i <= n; i ++ )//初始化 下标从1开始
    {
        p[i]=i;
        nums[i]=1;
    }
    while (m -- )
    {
        char c[5]; int a,b;
        cin>>c;
        //cout<<c<<endl;
        if(c[0]=='C')
        {
            cin>>a>>b;
            if(find(a)==find(b))
                continue;//如果本来两个结点就是连在一起的，则不需要再把联通结点个数相加
            //p[find(a)]=find(b); 应该先算结点个数再连起来
            nums[find(b)]+=nums[find(a)];
            p[find(a)]=find(b);
        }
        else if(c[1]=='1')//char*类型的字符串不能用“==”比较，只有string类可以，char*应该用strcmp比较
        {   
            cin>>a>>b;
            if(find(a)==find(b))
                cout<<"Yes"<<endl;
            else
                cout<<"No"<<endl;
        }
        else if(c[1]=='2')
        {
            cin>>a;
            cout<<nums[find(a)]<<endl;
        }
    }
}
  • char*类型的字符串不能用“==”比较，只有string类可以，char*应该用strcmp()比较
  • 记录结点数量增加时需要特判：如果本来两个结点就是连在一起的，则不需要再把联通结点个数相加
  • 两个集合合并时，应该先计算结点个数，再设置改变父结点

一道难题

AcWing 240. 食物链 视频讲解

并查集可以分为种类并查集（带权并查集）和拆点并查集

回顾并查集，最初的并查集是作为种类分类的集合，但是到后来的权值并查集显然就不是这个作用了，它通过以根为基准建立了一套偏移系，通过路径压缩，能够把每个元素的偏移直接与根连接上，查询就很容易计算。不在这个集合中的就先加进来。种类并查集只是有一个mod系的权值并查集，而且还比较好写。

  • 本题的种类并查集写法

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    58
    59
    60
    61
    #include <iostream>
    using namespace std;
    const int N = 50010;

    int n, m;
    int p[N], d[N];

    int find(int x)
    {
    	if (p[x] != x)
    	{
    		int t = find(p[x]);
    		d[x] += d[p[x]];
    		p[x] = t;
    	}
    	return p[x];
    }

    int main()
    {
    	scanf("%d%d", &n, &m);

    	for (int i = 1; i <= n; i++)
    		p[i] = i;

    	int res = 0;
    	while (m--)
    	{
    		int t, x, y;
    		scanf("%d%d%d", &t, &x, &y);

    		if (x > n || y > n)
    			res++;
    		else
    		{
    			int px = find(x), py = find(y);
    			if (t == 1)
    			{
    				if (px == py && (d[x] - d[y]) % 3)
    					res++;
    				else if (px != py)
    				{
    					p[px] = py;
    					d[px] = d[y] - d[x];
    				}
    			}
    			else
    			{
    				if (px == py && (d[x] - d[y] - 1) % 3)
    					res++;
    				else if (px != py)
    				{
    					p[px] = py;
    					d[px] = d[y] + 1 - d[x];
    				}
    			}
    		}
    	}
    	printf("%d\n", res);
    	return 0;
    }

  • 本题的拆点并查集写法（拓展域）

    一篇好的题解

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    58
    #include<bits/stdc++.h>
    using namespace std;

    const int maxn=50005;
    int fa[maxn*3];
    int n,m;
    int ans;

    int Find(int x){
        int t=x;
        while(fa[t]!=t) t=fa[t];
        while(x!=t)
        {
            int temp=fa[x];
            fa[x]=t;
            x=temp;
        }
        return t;
    }

    void Join(int x,int y){
        int fx=Find(x),fy=Find(y);
        if(fx!=fy)
            fa[fx]=fy;
    }

    int main(){
        scanf("%d%d",&n,&m);
        for(int i=1;i<=3*n;i++) fa[i]=i;
        for(int i=1;i<=m;i++){
            int num,a,b;
            scanf("%d%d%d",&num,&a,&b);
            if(a<1||a>n||b<1||b>n) {
                ans++; continue;
            }
            if(num==2&&a==b){
                ans++;continue;
            }
            if(num==1){//a,b同类
                if(Find(a)==Find(b+n)||Find(b)==Find(a+n)) ans++;//如果a吃b或者b吃a，说明是假话
                else {//否则是真话，建立a和b同类的关系
                    Join(a,b);
                    Join(a+n,b+n);
                    Join(a+2*n,b+2*n);
                }
            }
            else if(num==2){//a吃b
                if(Find(a)==Find(b)||Find(b)==Find(a+n)) ans++;//如果a,b同类或者b吃a，说明是假话
                else {//否则是真话，建立a吃b的关系
                    Join(a,b+n);
                    Join(a+n,b+2*n);
                    Join(a+2*n,b);
                }
            }
        }
        printf("%d\n",ans);
        return 0;
    }

堆

堆(Heap)是一棵完全二叉树

小根堆：每一个结点都小于等于左右儿子

大根堆：每一个结点都大于等于左右儿子

STL中的堆就是优先队列priority_queue

堆用数列存储时从下标1开始，避免2×0=0发生冲突

  • 堆中常用的几个操作

    up()和down()是将堆中元素上调、下调的函数

    下面操作都是基于用数组存储堆，数组的存储特性

    1
    2
    3
    4
    5
    heap[++size]=x;up(size);				//插入一个数
    heap[1];							   //求集合当中的最小值（小顶堆）
    heap[1]=heap[size--];down(1);			//删除堆中的最小值
    heap[k]=heap[size--];down(k);up(k);		//删除堆中的第k个元素
    heap[k]=x;down(k);up(k);			   //修改堆中的第k个元素

  • 建堆操作

    1
    2
    3
    //在此之前 已经把输入存入了数组h[n]中
    for(int i=n/2;i;i--)
        down(i);//这样建堆的时间复杂度是O(n)!!

  • down()的写法

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    void down(int u)//u是要down的结点的下标!!!!!!
    {
        int t=u;
        if(u*2<=nums&&h[u*2]<h[t])
            t=u*2;
        if(u*2+1<=nums&&h[u*2+1]<h[t])
            t=u*2+1;
        if(t!=u)//t记录的是u及其两个子结点中最小的那个的下标，当最小的不是根结点时交换
        {    
            swap(h[t],h[u]);
            down(t);
        }
    }

  • 模拟堆时要求做 删除/修改 第k个插入的数 的操作时 题目链接

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    58
    59
    60
    61
    62
    63
    64
    65
    66
    67
    68
    69
    70
    71
    72
    73
    74
    75
    76
    77
    78
    79
    80
    81
    82
    83
    84
    85
    86
    #include <iostream>
    #include <algorithm>
    using namespace std;

    const int N = 100010;

    int h[N], mk[N], km[N], cnt;
    //h[N]中的映射是 数组下标k-值value
    //mk[N]中的映射是 插入的次序m-数组中的下标k
    //km[N]中的映射是 数组中的下标k-插入的次序m
    //km和mk互为反函数

    void heap_swap(int a, int b)// 交换两个点，及其映射关系
    {
        swap(mk[km[a]],mk[km[b]]);
        swap(km[a], km[b]);
        swap(h[a], h[b]);
    }

    void down(int u)
    {
        int t = u;
        if (u * 2 <= cnt && h[u * 2] < h[t]) t = u * 2;
        if (u * 2 + 1 <= cnt && h[u * 2 + 1] < h[t]) t = u * 2 + 1;
        if (u != t)
        {
            heap_swap(u, t);
            down(t);
        }
    }

    void up(int u)
    {
        while (u / 2 && h[u] < h[u / 2])
        {
            heap_swap(u, u / 2);
            u >>= 1;
        }
    }

    int main()
    {
        int n, m = 0;
        scanf("%d", &n);
        while (n -- )
        {
            string op;
            int k, x;
            cin>>op;
            if (op=="I")
            {
                scanf("%d", &x);
                cnt ++ ;
                m ++ ;
                mk[m] = cnt, km[cnt] = m;
                h[cnt] = x;
                up(cnt);
            }
            else if (op=="PM") 
                printf("%d\n", h[1]);
            else if (op=="DM")
            {
                heap_swap(1, cnt);
                cnt -- ;
                down(1);
            }
            else if (op=="D")
            {
                scanf("%d", &k);
                k = mk[k];
                heap_swap(k, cnt);
                cnt -- ;
                up(k);
                down(k);
            }
            else
            {
                scanf("%d%d", &k, &x);
                k = mk[k];
                h[k] = x;
                up(k);
                down(k);
            }
        }
        return 0;
    }

哈希

一般哈希

哈希表有两种存储方法：开放寻址法和拉链法

840.模拟散列表 这道题用set也能做，但耗时会多许多

  • 拉链法就是用一个类似邻接表的空间存储，将要存的数据映射到邻接表中

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    #include <cstring>
    #include <iostream>

    using namespace std;

    const int N = 100003;

    int h[N], e[N], ne[N], idx;

    void insert(int x)
    {
        int k = (x % N + N) % N;//C++的取模规则：负数得到的模是负数，正数得到的模是正数
                                //这样取模可以保证 哈希值k 为正
        e[idx] = x;
        ne[idx] = h[k];
        h[k] = idx ++ ;
    }               

    bool find(int x)
    {
        int k = (x % N + N) % N;//C++的取模规则：负数得到的模是负数，正数得到的模是正数
                                //这样取模可以保证 哈希值k 为正
        for (int i = h[k]; i != -1; i = ne[i])
            if (e[i] == x)
                return true;

        return false;
    }

    int main()
    {
        int n;
        scanf("%d", &n);

        memset(h, -1, sizeof h);

        while (n -- )
        {
            char op[2];
            int x;
            scanf("%s%d", op, &x);

            if (*op == 'I') insert(x);
            else
            {
                if (find(x)) puts("Yes");
                else puts("No");
            }
        }

        return 0;
    }

  • 开放寻址法

    • memset()是按字节来格式化的，所以有了下面题目中的设置方式

      平时格式化为-1和0都是因为0的int型0的单个字节也是0，int型-1的单个字节也是-1

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    #include <cstring>
    #include <iostream>
    using namespace std;

    const int N = 200003, null = 0x3f3f3f3f;//这样声明是因为memset格式化是以字节为单位，而int为4个字节
    //null设置这么大是为了避免和给的数据重复，给的数据范围在正负1e9之间
    int h[N];

    int find(int x)
    {
        int t = (x % N + N) % N;
        while (h[t] != null && h[t] != x)
        {
            t ++ ;
            if (t == N) t = 0;
        }
        return t;
    }

    int main()
    {
        memset(h, 0x3f, sizeof h);//memset按字节格式化

        int n;
        scanf("%d", &n);

        while (n -- )
        {
            char op[2];
            int x;
            scanf("%s%d", op, &x);
            if (*op == 'I') h[find(x)] = x;
            else
            {
                if (h[find(x)] == null) puts("No");
                else puts("Yes");
            }
        }
        return 0;
    }

字符串哈希

可以做到一些KMP做不到的事情

模板代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
//核心思想：将字符串看成P进制数，P的经验值是131或13331，取这两个值的冲突概率低
//小技巧：取模的数用2^64，这样直接用unsigned long long存储，溢出的结果就是取模的结果

typedef unsigned long long ULL;
ULL h[N], p[N]; // h[k]存储字符串前k个字母的哈希值, p[k]存储 P^k mod 2^64

// 初始化
p[0] = 1;
for (int i = 1; i <= n; i ++ )
{
    h[i] = h[i - 1] * P + str[i];
    p[i] = p[i - 1] * P;
}

// 计算子串 str[l ~ r] 的哈希值
ULL get(int l, int r)
{
    return h[r] - h[l - 1] * p[r - l + 1];
}

例题 841.字符串哈希

3.搜索与图论

DFS/BFS

数据结构 空间
DFS stack O(h) 不具有最短性
BFS queue O(2^h) “最短路”

求最短等等一般用BFS

思路比较奇怪或者对空间有要求的一般用DFS


DFS：

例题：842. 排列数字

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include <iostream>
#include <cstring>
#include <algorithm>
//一定要想象树状结构
const int N = 10;
using namespace std;
int n,path[N];
bool st[N];

void dfs(int u)
{
    if(u==n)
    {
        for (int i = 0; i < n; i ++ )
            cout<<path[i]<<" ";
        puts("");
        return;
    }
    for (int i = 1; i <= n; i ++ )
    {
        if(!st[i])
        {
            st[i]=true;//提示后续的层这个数字已经用过了
            path[u]=i;
            dfs(u+1);
            st[i]=false;
        }
    }
}
int main()
{
    cin>>n;
    dfs(0);
    return 0;
}
  • 剪枝：遇到不合法的情况直接回溯
    • 最优解剪枝
    • 可行性剪枝

843. n-皇后问题

第一种：逐行枚举

预先分析出每一行一个皇后，所以可以按行来枚举，判断哪一列和哪一条对角线可行

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include <iostream>
#include <cstring>
#include <algorithm>
//一定要想象树状结构
const int N = 10;
using namespace std;
int n;
char g[N][N];
bool col[N],dg[N],udg[N];

void dfs(int u)
{
    if(u==n)
    {
        for (int i = 0; i < n; i ++ )
            puts(g[i]);
        puts("");
        return;
    }
    for (int i = 0; i < n; i ++ )//循环条件可能会变
    {
        if(!col[i]&&!dg[i+u]&&!udg[i-u+n])
        {
            col[i]=dg[i+u]=udg[i-u+n]=true;
            g[u][i]='Q';
            dfs(u+1);
            //复原
            col[i]=dg[i+u]=udg[i-u+n]=false;
            g[u][i]='.';
        }
    }
}
int main()
{
    cin>>n;
    for (int i = 0; i < n; i ++ )
        for (int j = 0; j < n; j ++ )
            g[i][j]='.';
    dfs(0);
    return 0;
}

第二种：逐格子枚举

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include <iostream>

using namespace std;

const int N = 20;

int n;
char g[N][N];
bool col[N], dg[N], udg[N];

void dfs(int u)
{
    if (u == n)
    {
        for (int i = 0; i < n; i ++ ) puts(g[i]);
        puts("");
        return;
    }

    for (int i = 0; i < n; i ++ )
        if (!col[i] && !dg[u + i] && !udg[n - u + i])
        {
            g[u][i] = 'Q';
            col[i] = dg[u + i] = udg[n - u + i] = true;
            dfs(u + 1);
            col[i] = dg[u + i] = udg[n - u + i] = false;
            g[u][i] = '.';
        }
}

int main()
{
    cin >> n;
    for (int i = 0; i < n; i ++ )
        for (int j = 0; j < n; j ++ )
            g[i][j] = '.';

    dfs(0);

    return 0;
}


BFS：可以搜到最短路（只有在所有边权都是1时才可行）

  • 例题： 844.走迷宫

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    #include <iostream>
    #include <algorithm>
    #include <queue>
    #include <cstring>//4
    using namespace std;
    const int N =  110;
    int map[N][N],status[N][N],m,n;
    typedef pair<int, int> PII;
    queue<PII> w;

    int bfs()
    {
        memset(status, -1, sizeof status);//1
        status[1][1]=0;
        w.push(make_pair(1,1));//3
        while(!w.empty())
        {
            int dx[4]={0,0,-1,1},dy[4]={1,-1,0,0};//2
            for(int i=0;i<4;i++)
            {
                auto x=make_pair(w.front().first+dx[i],w.front().second+dy[i]);//3
                if(x.first>0&&x.first<=n&&x.second>0&&x.second<=m&&status[x.first][x.second]==-1&&map[x.first][x.second]==0)//行和列要分清！！！
                {
                    w.push(x);
                    status[x.first][x.second]=status[w.front().first][w.front().second]+1;
                    //cout<<status[x.first][x.second]<<endl;
                }
            }
            w.pop();
        }
        return status[n][m];
    }
    int main()
    {
        cin>>n>>m;
        for(int i=1;i<=n;i++)
            for(int j=1;j<=m;j++)
                cin>>map[i][j];
        cout<<bfs();
    }

    • memset(status, -1, sizeof status);用于将某段内存全部设置为指定的值，使用时应该包含头文件#include <cstring>

    • 这类走迷宫问题，向四个方向走的便捷写法：

      1
      2
      3
      4
      5
      6
      int dx[4]={0,0,-1,1},dy[4]={1,-1,0,0};
      ...
      for(int i=0;i<4;i++)
      {
      	auto x=make_pair(a+dx[i],b+dy[i]);
      }

    • auto关键字还挺好用的，懒得写很长的类型名关键字时可以用auto

    • pair类型数据尽量用make_pair()来合并后赋值，直接用花括号{x,y}赋值，在给auto类型赋值时会被错误识别

  • 例题：845. 八数码

    这个题第一次写真的不好写，细节很多

    不错的题解，可以看看他的代码

    我的代码：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    #include <iostream>
    #include <algorithm>
    #include <queue>
    #include <unordered_map>//1
    using namespace std;

    unordered_map<string,int> status;
    queue<string> q;
    int dx[4]={0,0,-1,1},dy[4]={1,-1,0,0};//这个无所谓
    int bfs(string start)
    {
        string end="12345678x";
        q.push(start);
        int distance=0;
        while(!q.empty())
        {
            auto s=q.front();
            q.pop();
            distance=status[s];
            if(s==end)
                return distance;
            int k=s.find('x');
            int x=k/3,y=k%3;//(x,y)//建系方式//2
            for(int i=0;i<4;i++)
            {
                int px=x+dx[i],py=y+dy[i];
                //cout<<x<<" "<<y<<" ";
                //cout<<px<<" "<<py<<endl;
                if(px>=0&&px<3&&py>=0&&py<3)//这个if语句体很关键//3
                {
                    swap(s[k],s[px*3+py]);
                    //cout<<s<<endl;
                    //cout<<status.count(s)<<endl;
                    if(!status.count(s))
                    {
                        q.push(s);
                        status[s]=distance+1;
                        //cout<<status[s]<<endl;
                    }
                    swap(s[k],s[px*3+py]);//记得复原
                }
            }
        }
        return -1;
    }

    int main()
    {
        string start,c;
        for (int i = 0; i < 9; i ++ )
        {
            cin>>c;
            start+=c;
        }
        cout<<bfs(start);
        return 0;
    }

    • 一定要分清x和y

      在这里约定（以后尽量都这样写）：x和y与二维直角坐标系中的x和y是同一个概念，x是横坐标，y是纵坐标，x是列数，y是行数

    • dist数组：将矩阵状态压缩为一个字符串，利用unordered_map<string,int> status;来实现：每种矩阵状态与一个数的一一对应关系，不同的字符串区分不同的矩阵，从而避免在同一个矩阵中循环

    • 用unordered_map而不用map的原因：用map会超时

树与图

  • 树是无环连通的图
  • 图分为有向图和无向图，在算法题中，无向图可以通过一条边上建立两条路径来实现，所以无向图可以看做一种特殊的有向图

树和图的存储

  • 有向图的存储：

    邻接矩阵：二维数组实现，空间复杂度O(n^2)，比较适合稠密图

    邻接表：单链表实现，每个节点后面都要跟一个单链表

  • 邻接表用数组实现（可以用vector实现但效率没有数组高），相当于n个单链表

    单链表的数组表示法见此文章

    邻接表就是再多用一个数组来存n个单链表表头的地址

    1
    2
    3
    4
    5
    6
    7
    int h[N],e[M],nx[M],idx;
    //idx是下一个元素的地址；h数组存放表头地址；e数组相当于内存，下标是地址，值是对应地址处的内容；nx数组存放的是地址为idx处的节点的next节点的地址
    //在一个单链表中h只是单个的地址，表示表头地址
    void add(int a,int b)
    {
    	e[idx]=b,nx[idx]=h[a],ha=idx++;
    }

树和图的遍历

DFS：

846.树的重心：题解参考这里

  • 自己的代码：真的不好写..

    • 这题要建无向图，所以邻接表中要add(a, b),add(b,a);
    • memset(h, -1, sizeof h);格式化某段内存
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    #include <iostream>
    #include <cstring>
    #include <algorithm>
    using namespace std;

    const int N = 1e5+10;
    int n,ans=N;
    bool st[N];
    int h[N], e[N*2],nx[N*2],idx;
    void add(int a,int b)
    {
        e[idx]=b;
        nx[idx]=h[a];
        h[a]=idx++;
    }
    int dfs(int u)
    {
        st[u]=true;
        int sum=1,res=0;//sum是以u为根的树的节点个数，res是目前u的最大子树的节点个数
        for(int i=h[u];i!=-1;i=nx[i])
        {
            int j=e[i];//i是地址，j是点（以某个数字为标号）
            if(!st[j])
            {
                int s=dfs(j);
                res=max(res,s);
                sum=sum+s;
            }
        }
        //cout<<u<<sum;
        res=max(res,n-sum);
        ans=min(res,ans);
        return sum;
    }
    int main()
    {
        memset(h, -1, sizeof h);//一定要初始化链表头数组为-1，表示最开始是空的邻接表
        cin>>n;
        for (int i = 0; i < n-1; i ++ )
        {
            int a,b;
            cin>>a>>b;
            add(a, b),add(b,a);
        }
        dfs(1);
        cout<<ans;
        return 0;
    }

BFS：

847.图中点的层次：同样可以学一手代码规范

只能说BFS比DFS好写太多了，在不用剪枝只用暴搜的前提下

递归确实不好理解

拓扑排序

5.动态规划

  • 常用的：
    • 背包问题
    • 线性DP
    • 区间DP
  • 思考dp和dfs之间的差异

背包问题

01背包问题

给定N个物品，和体积为V的背包。每个物品的体积为vi，价值为wi，每件物品最多只能用1次

问在背包装得下的前提下，选出物品的价值最大是多少

  • 例题：AcWing 2. 01背包问题

    • 在这就体会到dp和dfs的差异所在了

      使用dfs遍历会超时

      dp主要运用了预处理的思想，而dfs则是类似于白手起家，一步步探索

      且dp使用了记忆化的技巧，后续计算会用到之前的结果

    • dp的代码

      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      16
      17
      18
      19
      20
      21
      #include <iostream>
      #include <utility>
      using namespace std;
      const int N = 1010;
      int n,m;
      pair<int,int> item[N];
      int f[N][N];//f[i][j]表示：【在前i个物品中选择&剩余体积为j】时 的 最大价值
      int main()
      {
          cin>>n>>m;
          for (int i = 1; i <= n; i ++ )
              cin>>item[i].first>>item[i].second;
          for (int i = 1; i <= n; i ++ )
              for (int j = 1; j <= m; j ++ )
              {    
                  f[i][j]=f[i-1][j];
                  if(j>=item[i].first)//
                      f[i][j]=max(f[i][j],f[i-1][j-item[i].first]+item[i].second);
              }
          cout<<f[n][m];
      }

    • 转换成一维：

      f(i)只用到了f(i-1)的状态，所以可以用滚动数组来做

      • 逆序遍历
      • 空间复杂度可以降低一半
      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      16
      17
      18
      void test_1_wei_bag_problem() {
          vector<int> weight = {1, 3, 4};
          vector<int> value = {15, 20, 30};
          int bagWeight = 4;

          // 初始化
          vector<int> dp(bagWeight + 1, 0);
          for(int i = 0; i < weight.size(); i++) { // 遍历物品
              for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
                  dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
              }
          }
          cout << dp[bagWeight] << endl;
      }

      int main() {
          test_1_wei_bag_problem();
      }

完全背包问题

与01背包不同的是每个物品有无限个

  • 朴素做法：只需要比01背包多一层循环，遍历：选择0~k个第i个物品时的不同情况，取最大的即可

    1
    2
    3
    4
    for(int i=1;i<=n;i++)
        for (int j=0;j<=weight;j++)
            for(int k=0;k*v[i]<=j;k++)
                f[i][j]=max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);

  • 优化做法：

    少一层循环，耗时可以降为五分之一

    1
    2
    3
    4
    5
    6
    7
    for(int i=1;i<=n;i++)
        for (int j=0;j<=weight;j++)
        {
            f[i][j]=f[i-1][j];
            if(j>=v[i])
                f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i]);
        }

  • 终极写法（降低为一维）：

    1
    2
    3
    4
    5
    for(int i=1;i<=n;i++)
        for (int j=v[i];j<=weight;j++)
        //完全背包问题利用滚动数组降低为一维时
        //由于与状态转移方程相同，所以不用倒序遍历                              
                f[j]=max(f[j],f[j-v[i]]+w[i]);

    与01背包的降维对比

    01：从大到小正序遍历体积

    完全：从小到大倒序遍历体积

    联想下面两者不同的状态转移方程

  • 完全背包和01背包

多重背包问题

每个物品有有限个，个数为si

  • 朴素做法和完全背包差不多，例题

  • ==利用二进制优化方法，可以将复杂度从N V S优化为N V logS==

二进制优化思想：

将物品打包，以二的幂次为单位，每个新物品只能用一次，转化为01背包问题

每个新物品体积为打包后的数量乘单个的体积，价值为打包后的数量乘单个的价值

例题

  • 代码如下：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    #include <iostream>
    using namespace std;
    const int N = 12010, M = 2010;

    int n, m;
    int v[N], w[N];
    int f[M];

    int main()
    {
        cin >> n >> m;

        int cnt = 0;
        //打包的过程
        for (int i = 1; i <= n; i ++ )
        {
            int a, b, s;
            cin >> a >> b >> s;
            int k = 1;
            while (k <= s)
            {
                cnt ++ ;
                v[cnt] = a * k;
                w[cnt] = b * k;
                s -= k;
                k *= 2;
            }
            if (s > 0)
            {
                cnt ++ ;
                v[cnt] = a * s;
                w[cnt] = b * s;
            }
        }

        n = cnt;//物品数量变少
        //与01背包问题等价
        for (int i = 1; i <= n; i ++ )
            for (int j = m; j >= v[i]; j -- )
                f[j] = max(f[j], f[j - v[i]] + w[i]);

        cout << f[m] << endl;

        return 0;
    }

分组背包问题

每一组中物品互斥

三层循环即可

核心代码：

1
2
3
4
5
for(int i=1;i<=n;i++)
    for(int j=m;j>=0;j--)
        for(int k=1;k<=s[i];k++)
            if(j>=v[i][k])
                f[j]=max(f[j],f[j-v[i][k]]+w[i][k]);

线性DP