社会网络复习

每一章后面的要点，对照“要点”回顾内容

1~3章 图论 联系

• 三元闭包理论：如果两人在社会网络中有一个共同的朋友，则他们俩将来成为朋友的可能性提高。

  两个人的共同朋友越多，则他们成为朋友的可能性越高

  两个人与共同朋友的关系越密切，则他们成为朋友的可能性越高

• 三元闭包的衡量标准——节点的聚集系数：A的任意两个朋友之间也是朋友的概率

  聚集系数计算方法

  

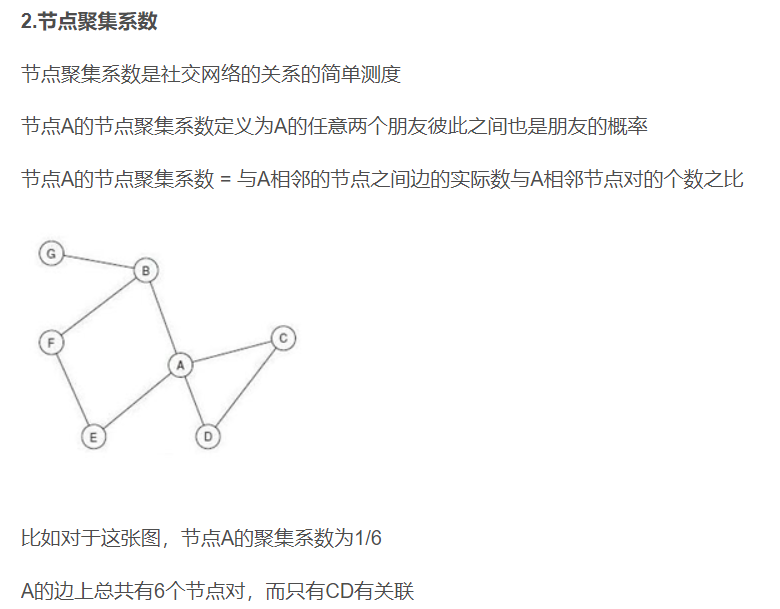
• 强三元闭包原理（假设）

  如果A-B和A-C之间的关系为强关系；则B-C 之间形成边的可能性应该很高；

• 桥、捷径的定义

  捷径：

  若边A-B的端点A和B没有共同的朋友，则称边A-B为捷径

  若删除该边，A和B的距离增加至2以上，则该边为捷径

  捷径的跨度为改变两端点在没有该边情况下的实际距离

  一个图中，已知A和B相连，若去掉连接A和B的边会导致A和B分属不同的连通分量，则将该边称为桥

• 证明：（反证法）在社交网络中，若节点A满足强三元闭包性质，并至少两个强联系边与之相连，则与其相连的任何捷径均为弱联系

• 边（A,B）的邻里重叠度

  捷径 = 邻里重叠度为0的边

  

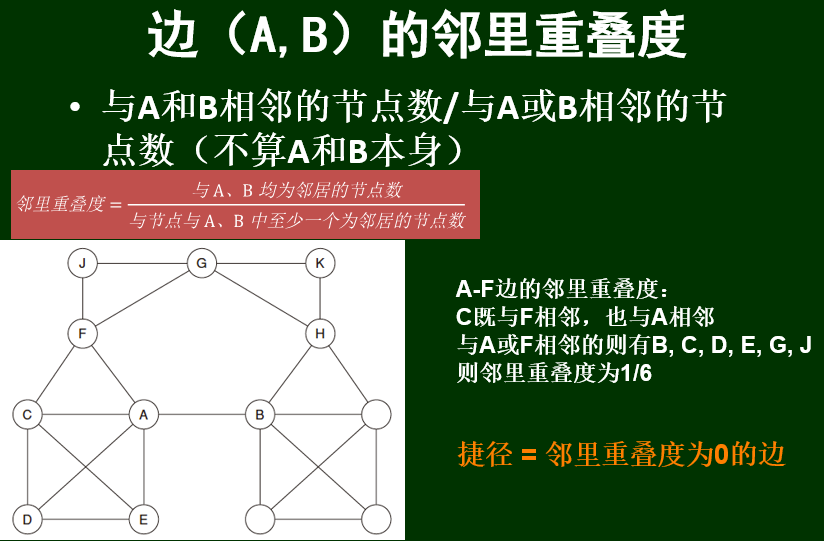
• 结构洞

• 划分图：

  一种是根据介数的划分方法：Newman方法,

  • 介数：

    

  • 通过每次删去图中介数最大的边，来实现对图的划分，介数最大的边，即为最关键的边。许多节点之间的的最短路径都要经过他

  • 介数计算的一种方法：

    • 从一个节点（A）开始，做宽度优先搜索，将节点分层（以便于下面的步骤）
    • 确定从A到其他每个节点的最短路径的条数
    • 确定当从节点A沿最短路径向其他所有节点发送1个单位流量时，经过每条边的流量。

    对每一个节点，重复上述过程，累计，除以2，即得每条边的介数。

    例子：

    每个点除了下面的点还给他的值之外，还有A发送的一个单位的信息流

    

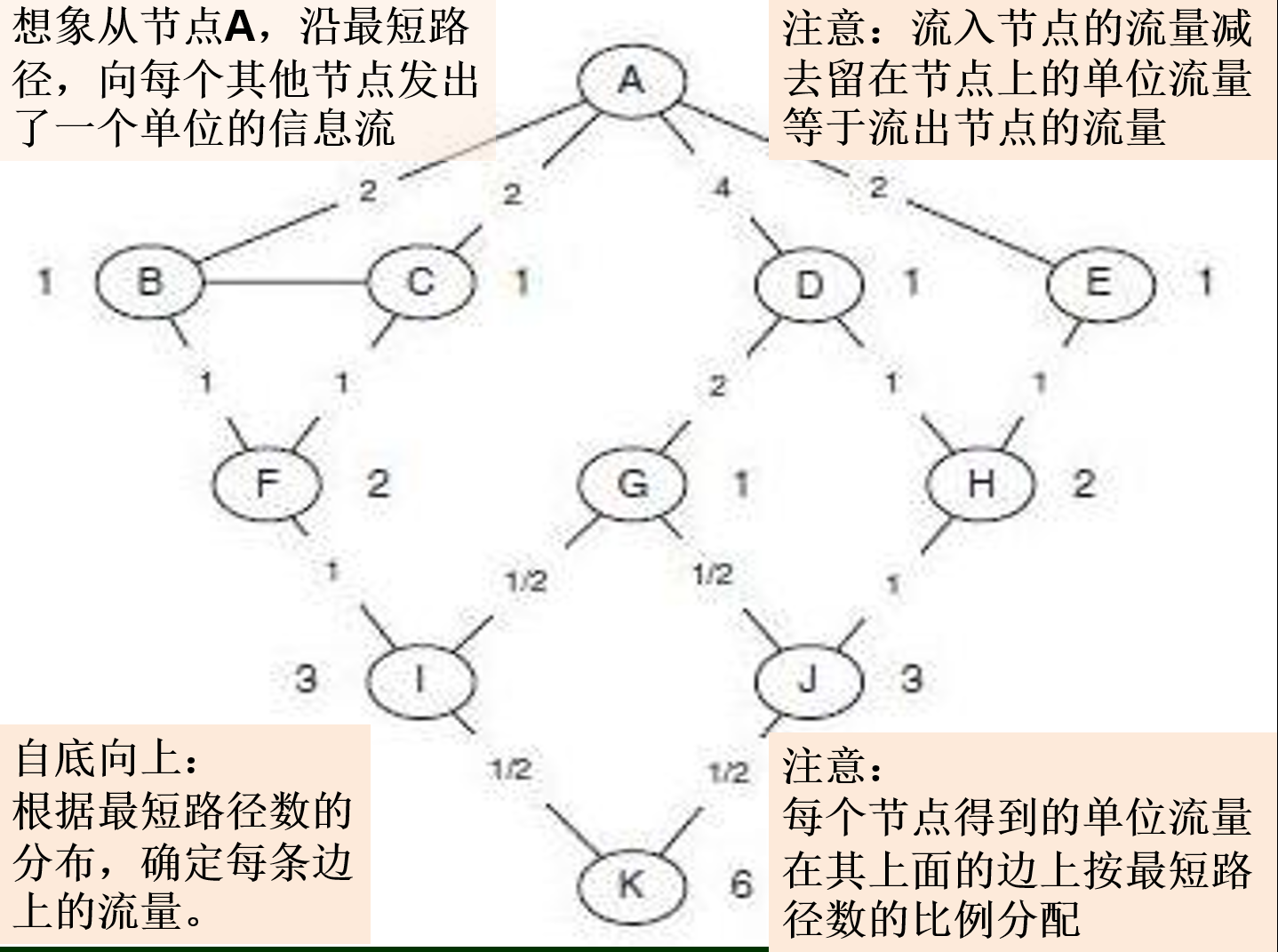
4章 同质性

• 同质性：

  定义：我们和自己的朋友间往往会有相同的特点，即社交网路中互相连接的人倾向于相似

  量化标准：

  

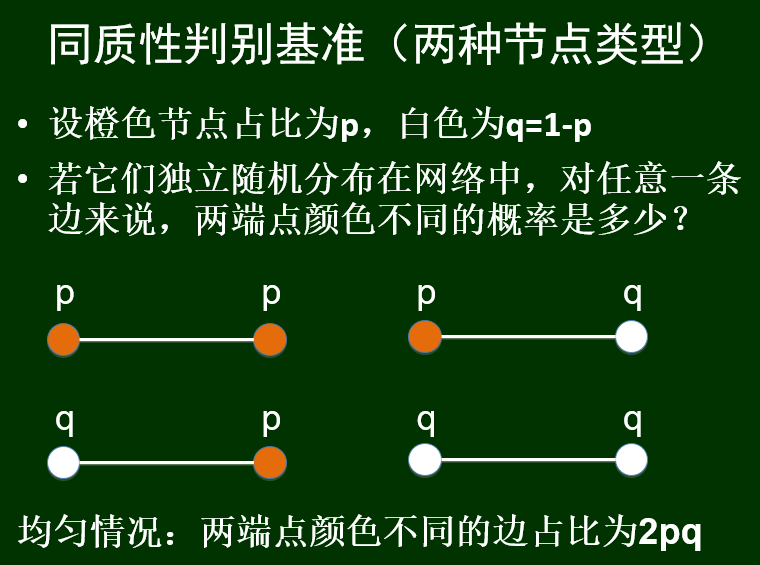
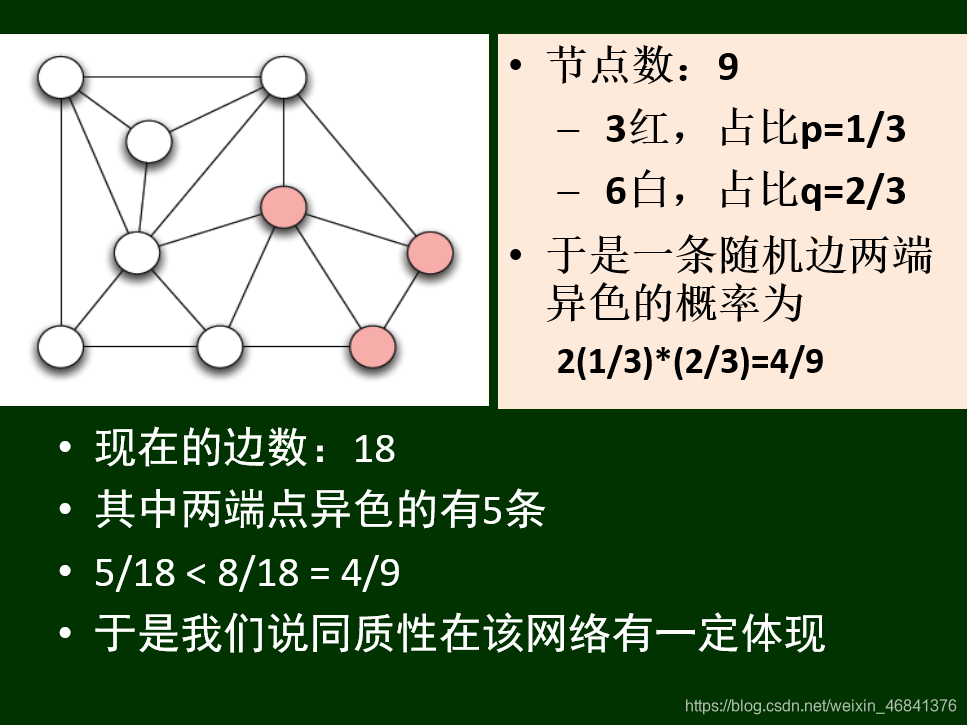
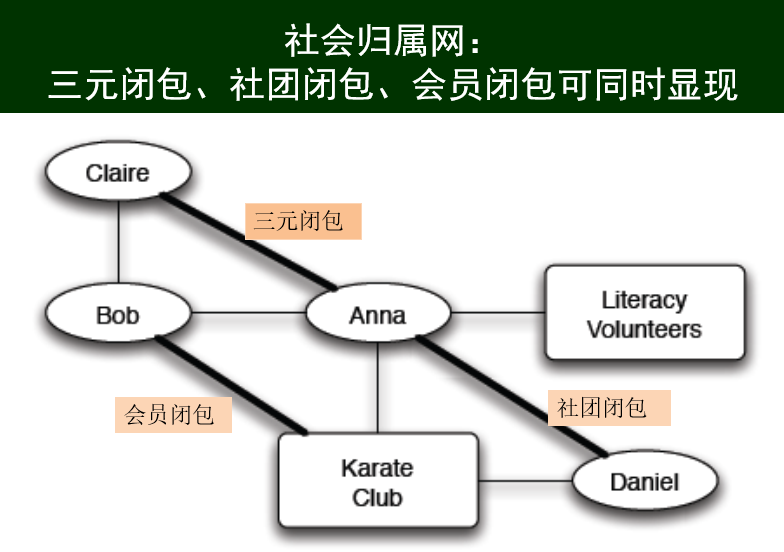
• 三种闭包：三元闭包、会员闭包、社团闭包

  

  • 例子：

    

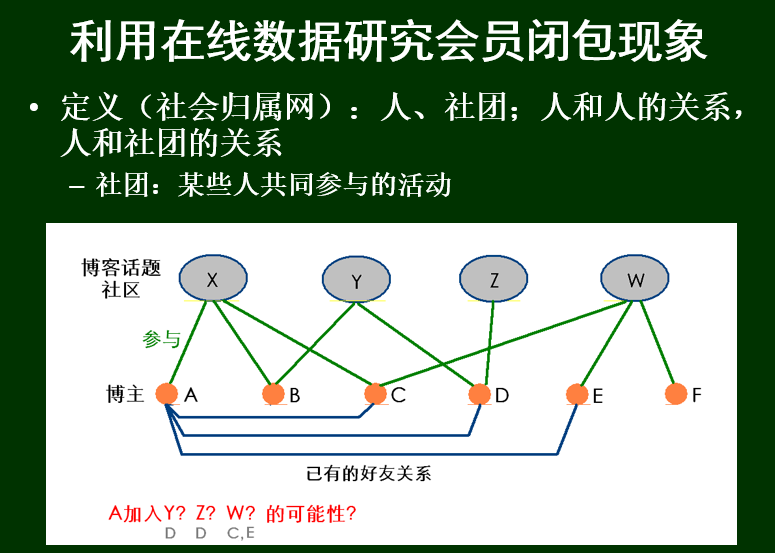
    A加入W可能性更高，因为有两个好友D,E都在W

• 朋友间相似的原因：选择（selection），影响（influence）

  

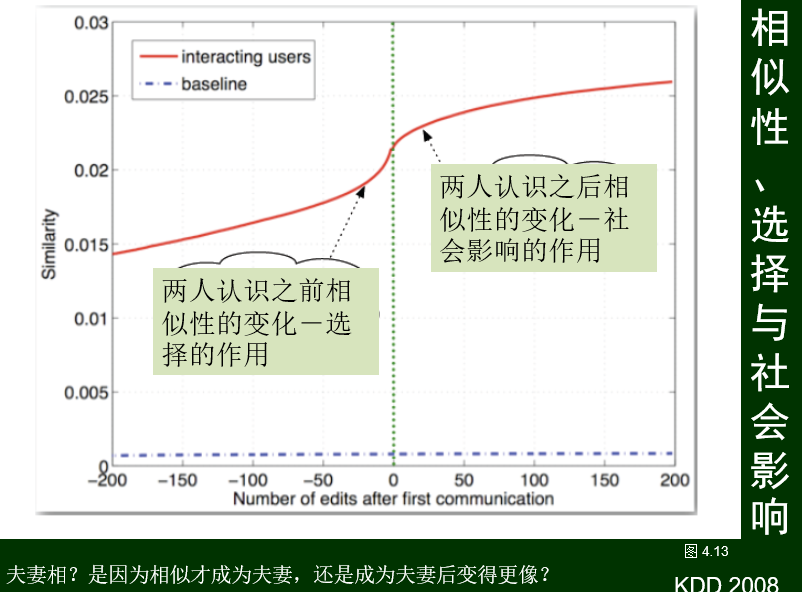
  如下图：选择对应社团闭包，影响对应会员闭包

  

• 隔离：同质化影响下发生的过程

  谢林模型：隔离的一种空间模型

  同质性影响结果：固有特质相同->可变特质趋同

5章 结构平衡 正负关系

• 边的正负性

  

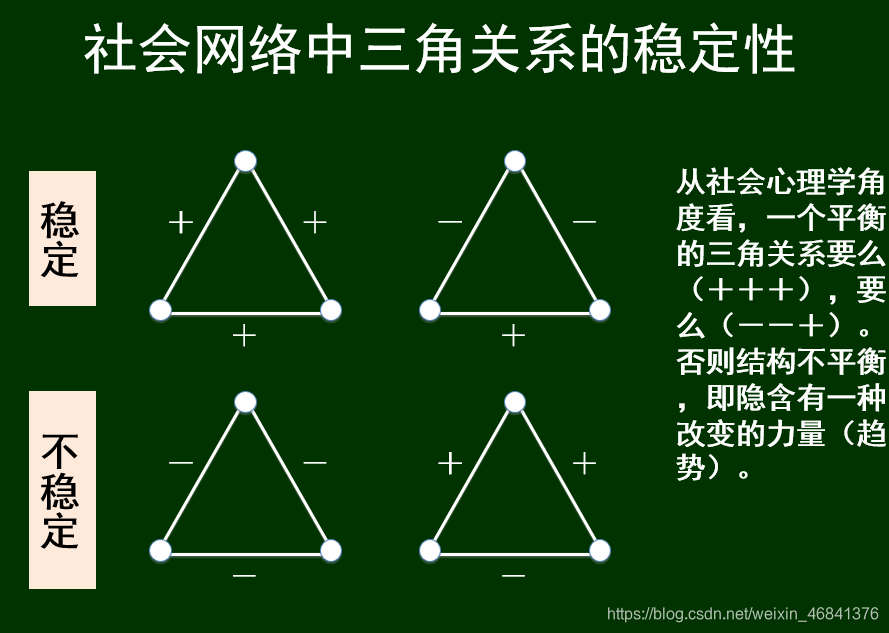
  只有+++和+--两种关系是稳定的

• 社会网络的结构平衡：（完全）图的结构是平衡的，若其中所有三角关系都是平衡的（即每个三角关系要么3＋，要么1＋和2－）。

  • 平衡定理

    如果一个标记的完全图是平衡的，则要么它的所有节点两两都是朋友，要么它的节点可以被分为两个组X和Y，其中X组内的节点两两都是朋友，Y组内的节点两两也是朋友，而X组中的每个节点都是Y组中每个节点的敌人

• 非完全网络（允许一些边的缺失）中的结构平衡;

  • 可以通过补充缺失的边（带符号），成一个平衡网络（这和完全图的平衡定义一致）
  • 节点可以分成两组（组内边为＋，跨组为－）
    这和平衡定理中给出的宏观结论一致（两个阵营）

  两个定义是等价的：

  

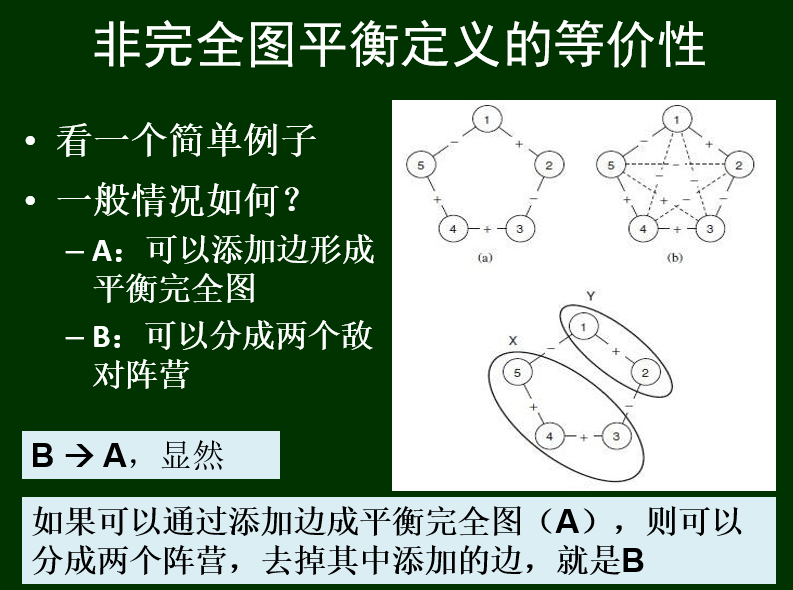
• 网络是否平衡的一个判断方法：一个标注图是平衡的，当且仅当它不包含有奇数个负关系的边的圈

• 将每个联通子图抽象为超结点，超结点之间以-连接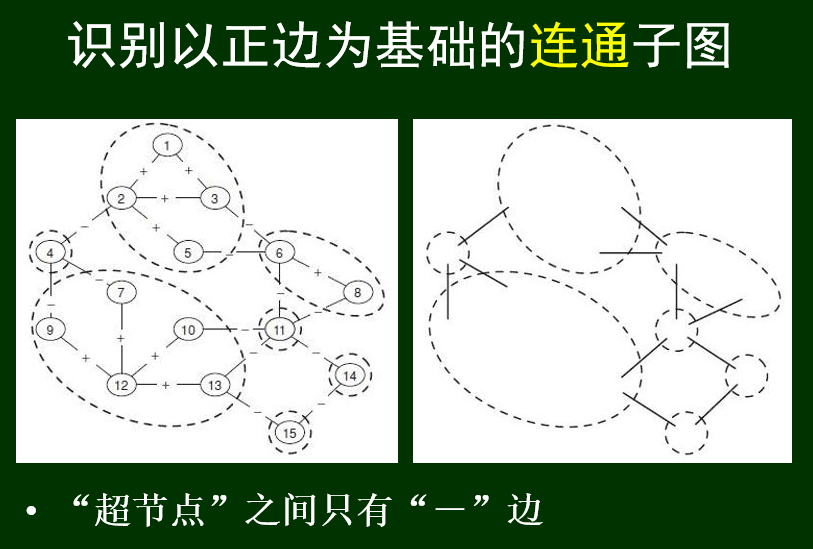

  

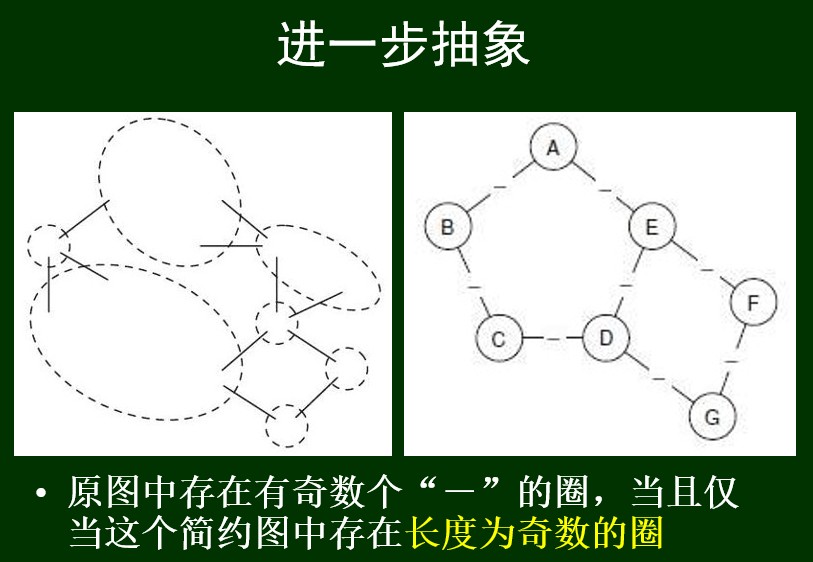
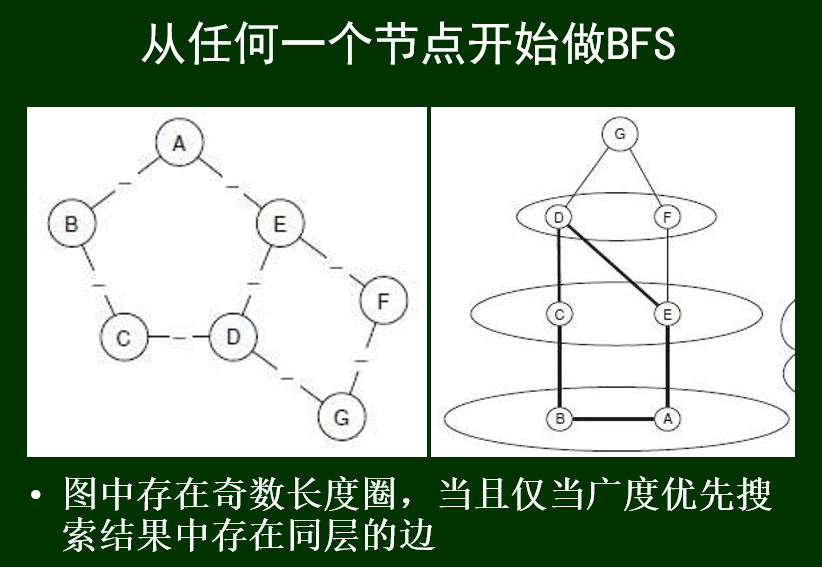
  图中存在奇数长度圈，当且仅当广度优先搜索结果中存在同层的边

6章 博弈

博弈三要素：参与人，策略（概率），收益

• 几种经典的模型：考试-报告博弈，囚徒困境，兴奋剂博弈，营销博弈

• 最佳应对-占优策略（严格/不严格）：

  

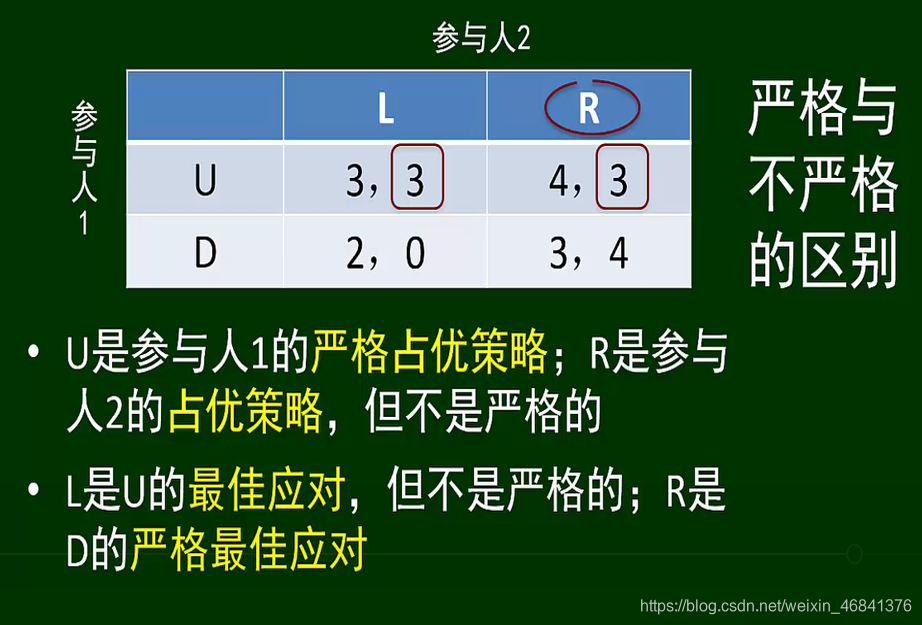
  占优策略的概念是相对于对方所有策略而言的，而最佳应对是针对单个策略而言。

• 

• 无占优策略例子（三客户博弈）

  引出纳什均衡：两个策略互为最佳应对

  

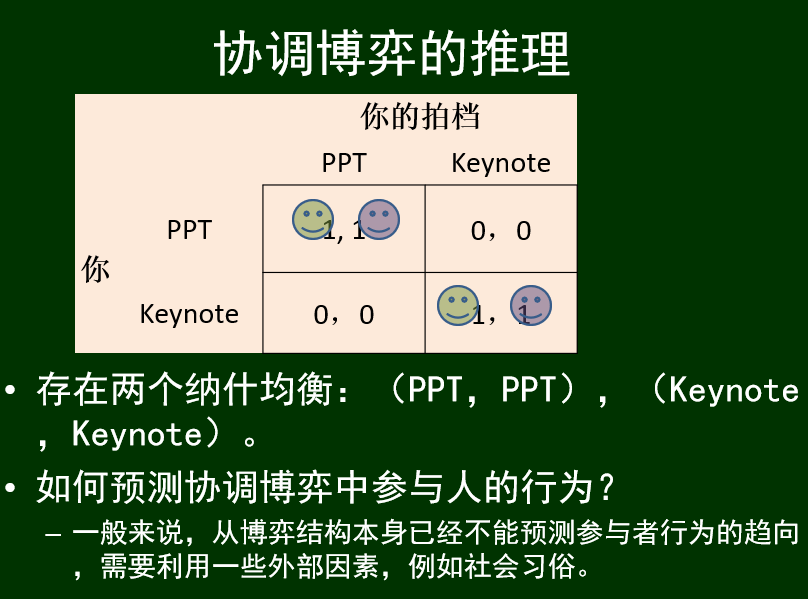
• 多重均衡（存在多组纳什均衡）-协调博弈

  例子：PPT制作（对等）

  

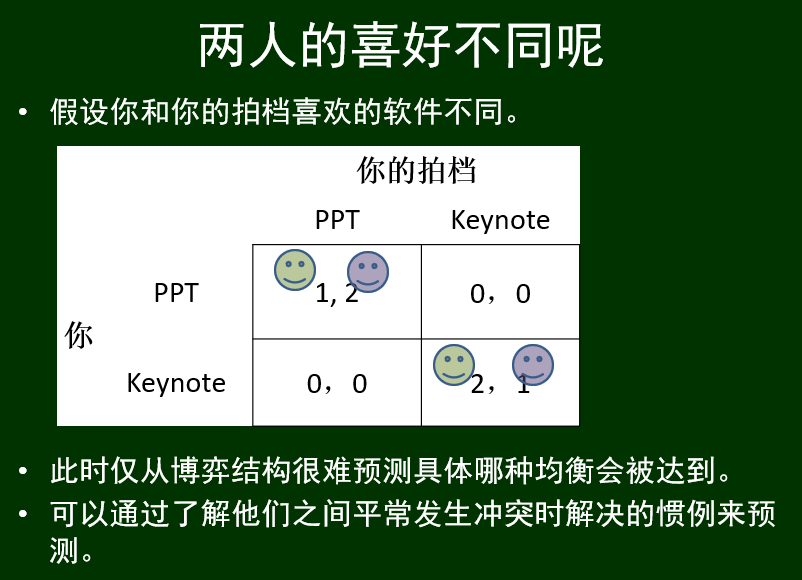
  • 不对等协调博弈：

    

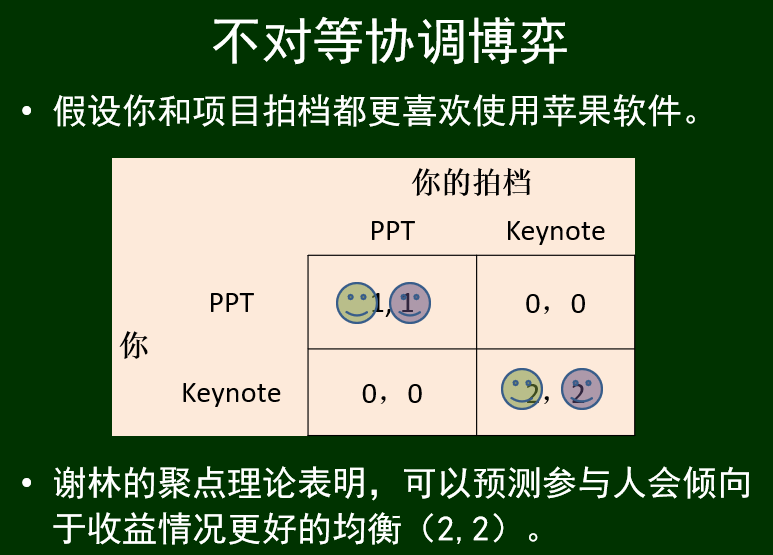
  • 两人喜好不同时：

    

• 猎鹿博弈：

  

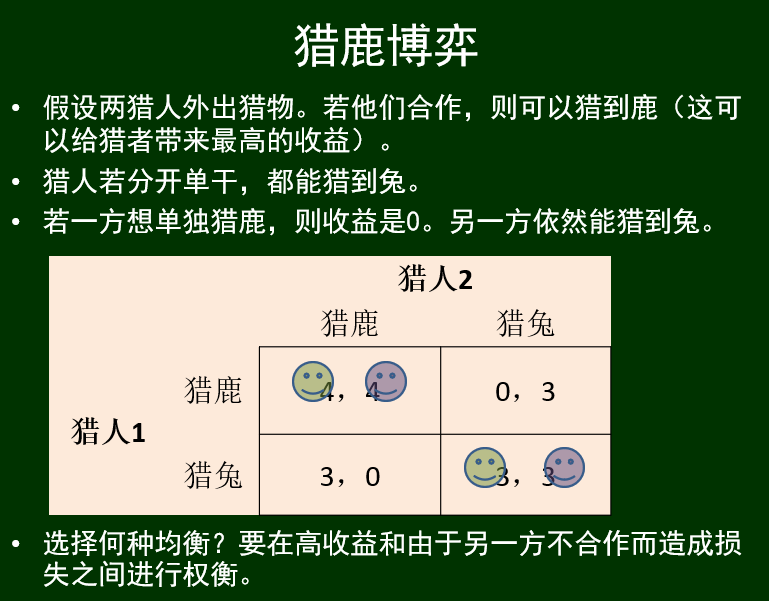
  要在高收益和由于另一方不合作而造成损失之间进行权衡。

• 鹰鸽博弈：

  

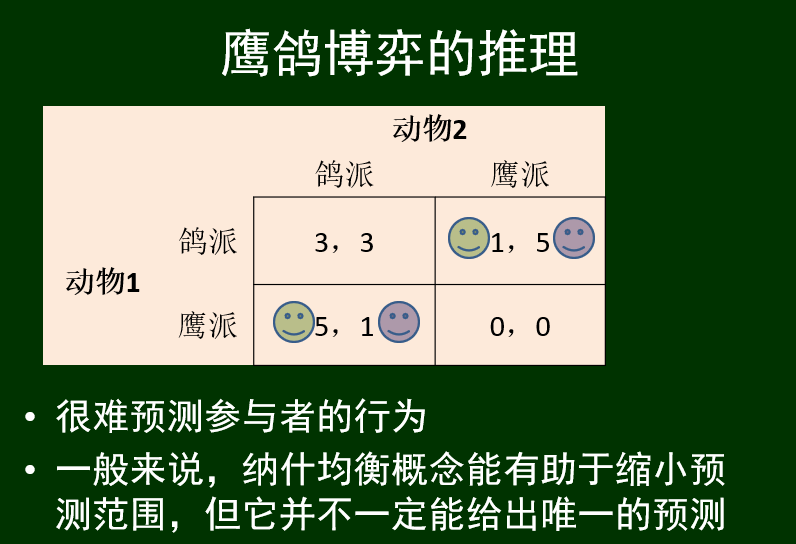
• 一般来说，纳什均衡的概念能有助于缩小预测范围，但它不一定能给出唯一的预测

• 

• 硬币博弈—零和博弈（不存在纳什均衡）

  

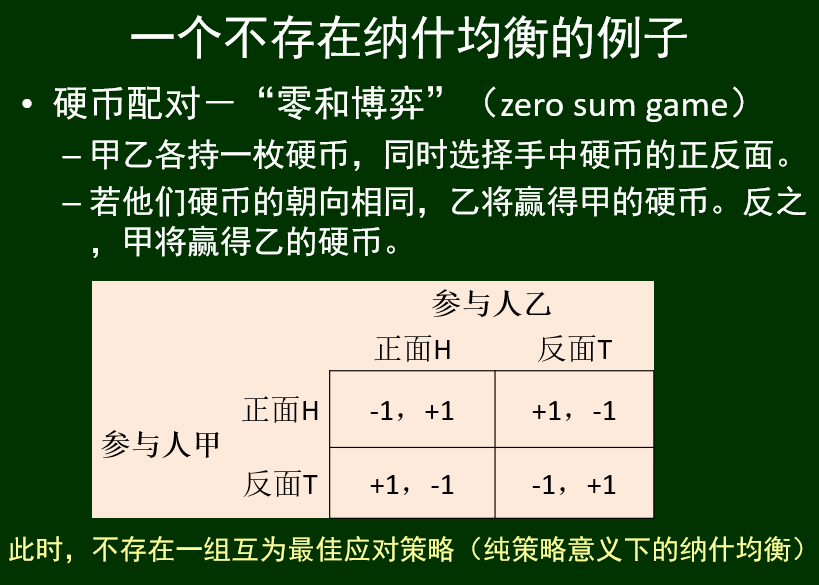
• 混合策略，引入概率

  

  混合策略互为最佳应对的必要条件

  

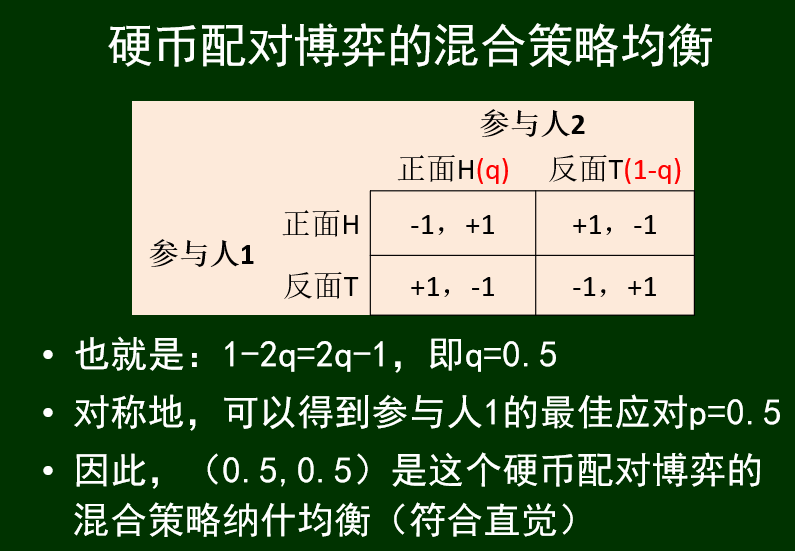
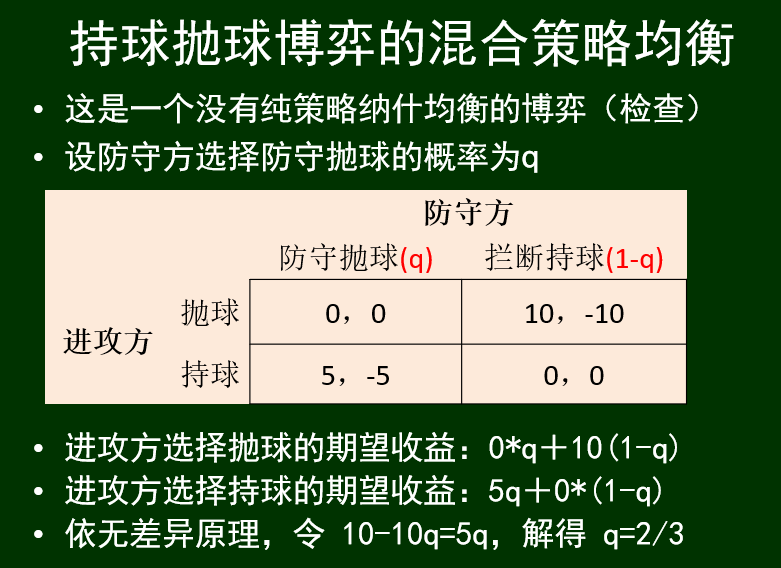
  再来一个混合策略均衡的例子：持球抛球博弈：

  

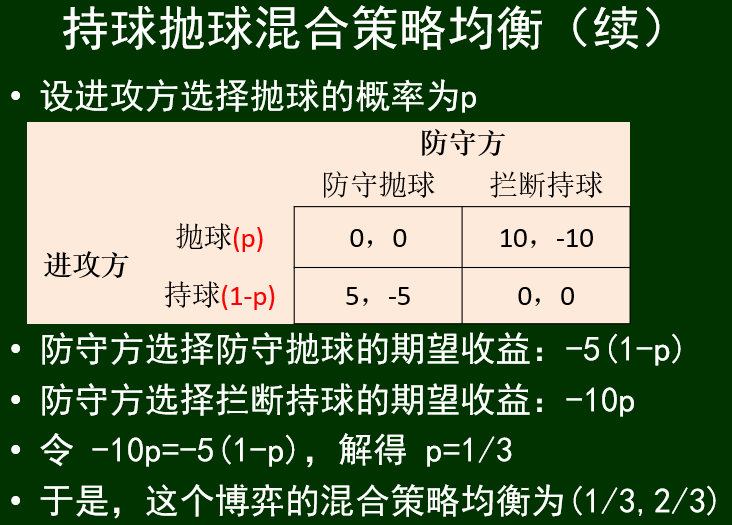
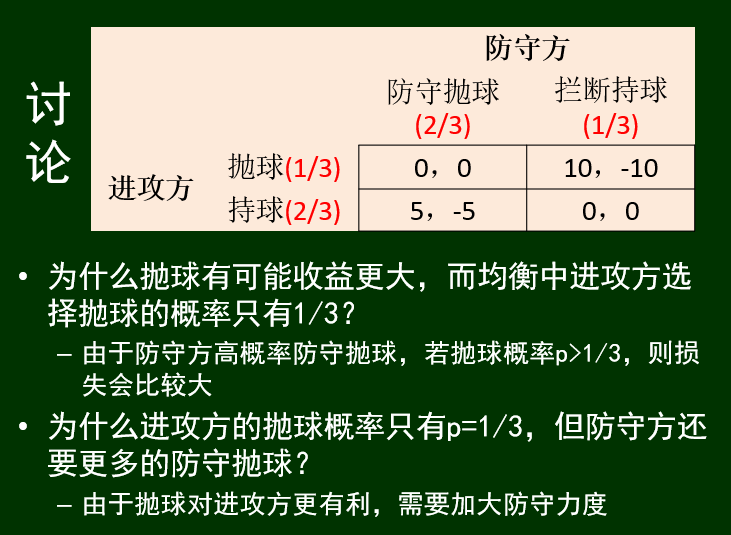
  讨论：

  

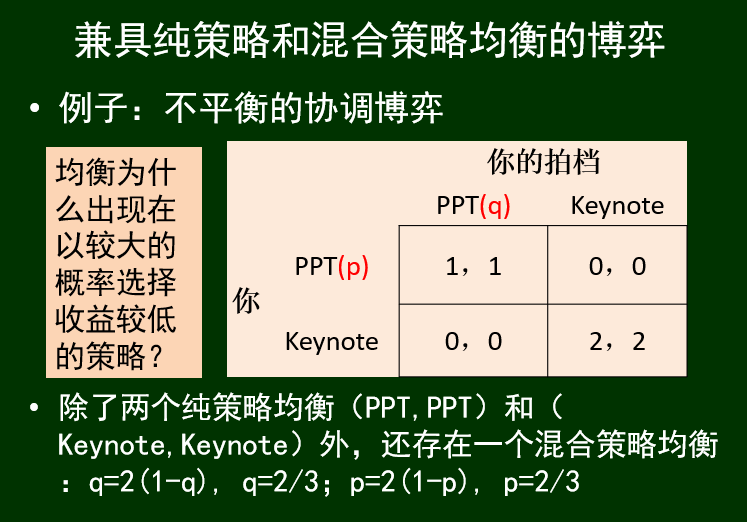
  【兼具纯策略和混合策略均衡的博弈】

  好的概率策略是使对方不知道用那个纯策略更好的策略

  

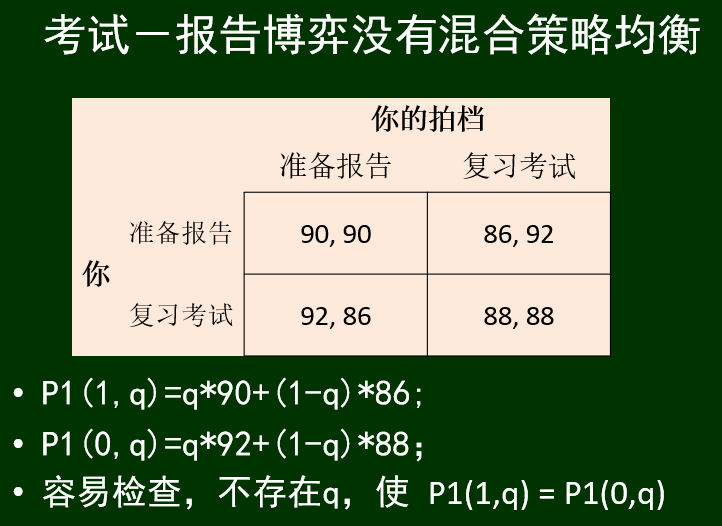
  • 没有混合策略均衡的纯策略博弈：

    

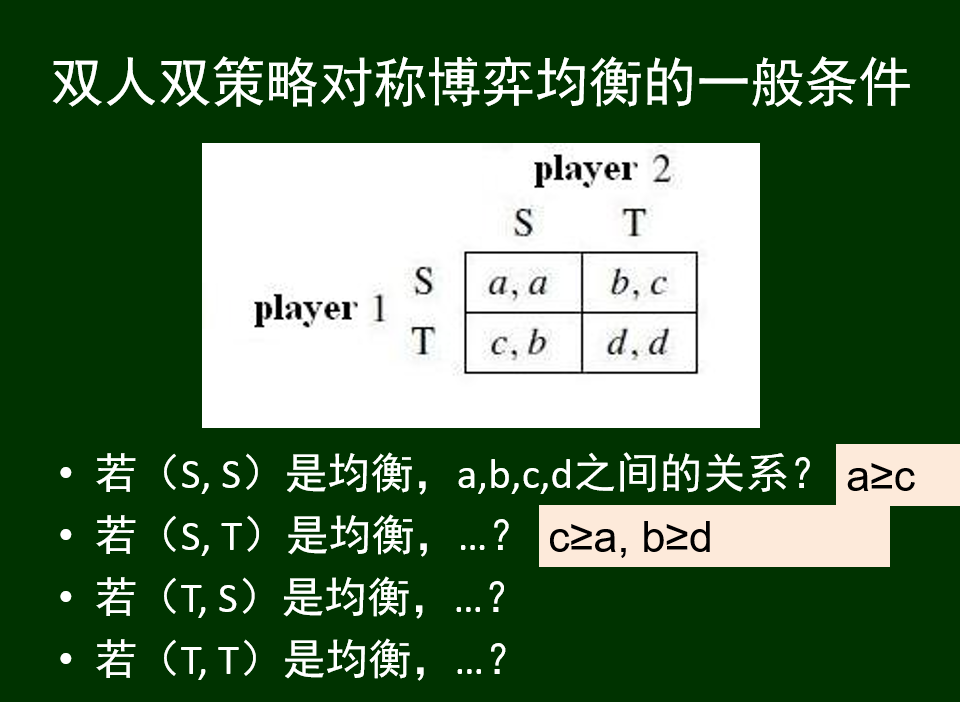
• 双人双策略博弈均衡的一般求法

  

• 一组策略选择是社会最优的（或社会福利最大化），若它使参与者的回报之和（总收益）最大。

  

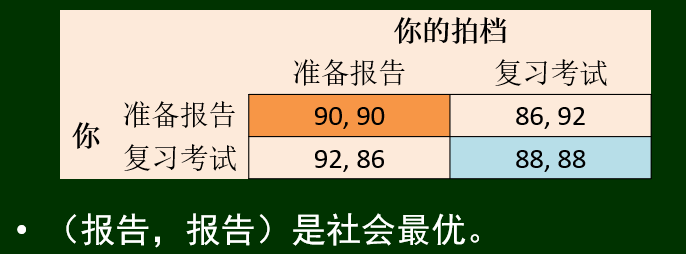
  社会最优和纳什均衡有可能一致，此时是理想系统

7章 进化博弈论

这章不太懂

对博弈论的推广——进化博弈论

• 囚徒困境：

  • 均衡出现在双方采用某一种相同的策略

  • 对应社会最优的策略组不是均衡，因为参与人之一有动机改变策略

• 鹰鸽博弈：

  • 均衡出现在双方采用不同的策略

• 进化稳定策略考察例子：

  还是引入概率，计算期望

  • 大体型：

    

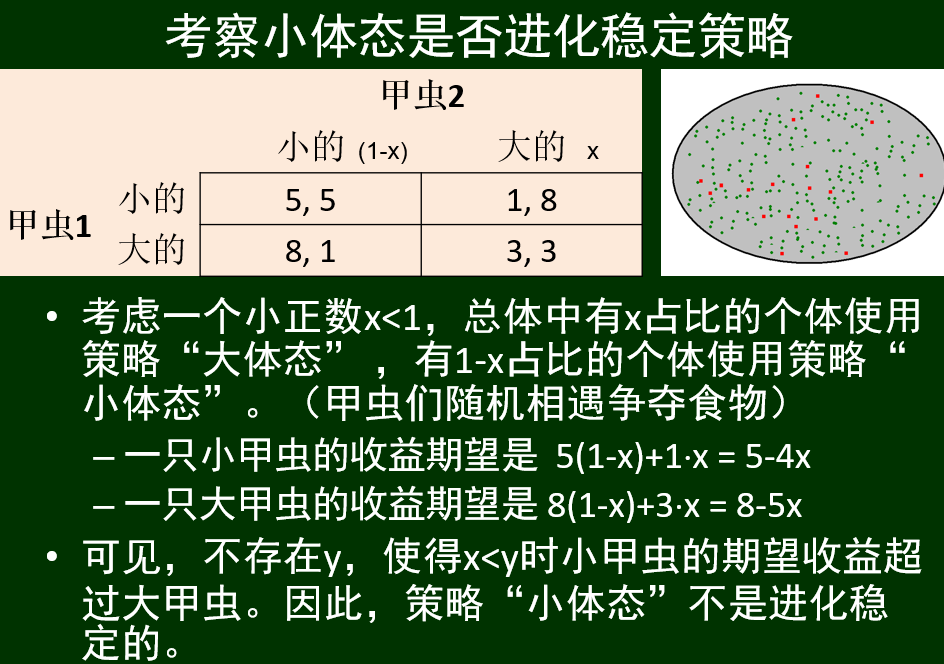
  • 小体型：

    

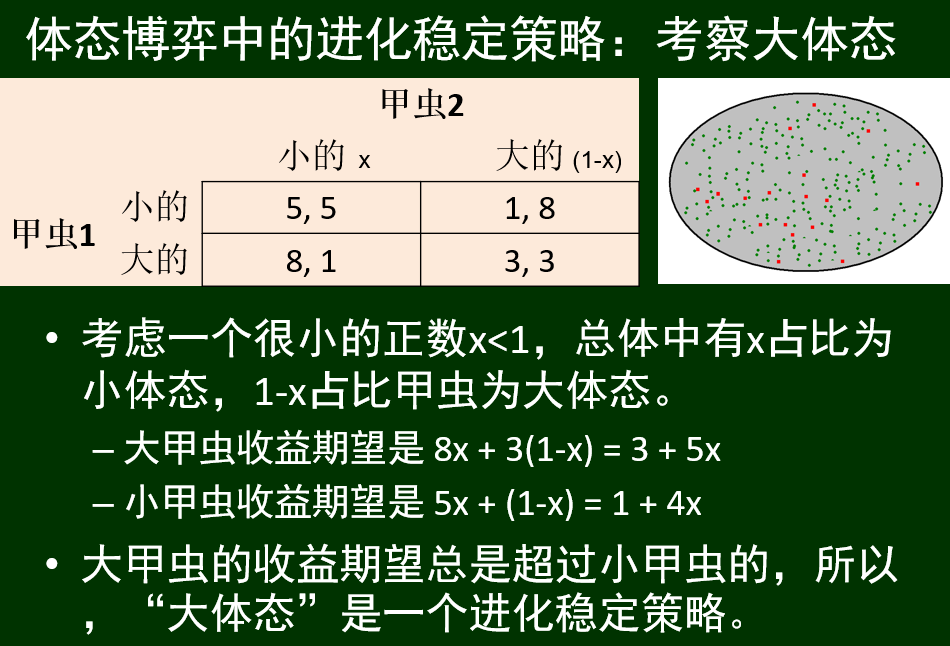
• 生物学家认为在自然界中存在具有囚徒困境结构的进化博弈现象

  例如病毒之间的进化博弈，类似囚徒困境

  

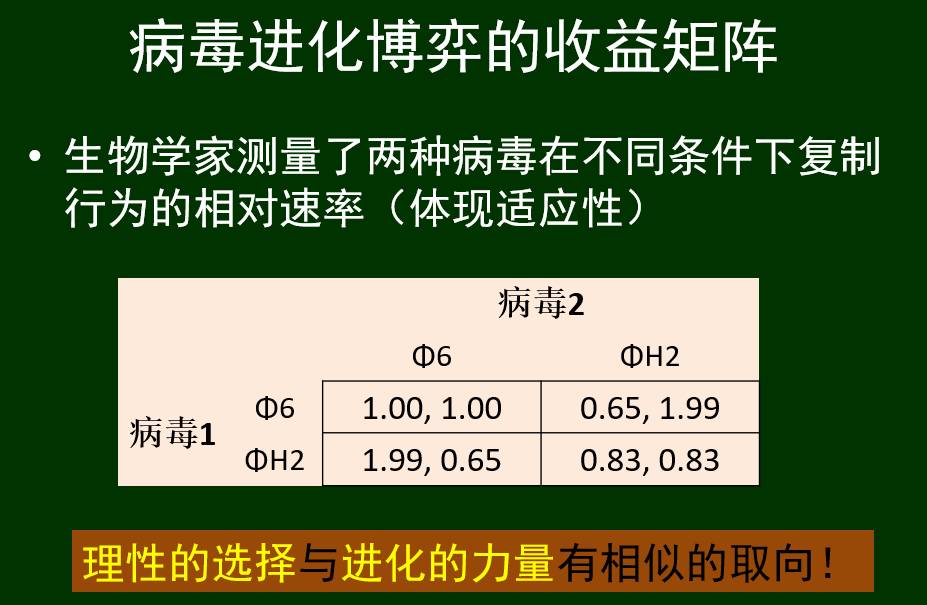
• 进化博弈论小结:

  

8章 网络流量博弈论

• 均衡的流量，布雷斯悖论

• 根据潜能的概念，借助动态规划

  

• 要点：

  

9章 拍卖博弈论

• 四种拍卖：英式拍卖（买家从低到高报价），荷兰式拍卖（卖家从高到低出价）

  次价密封拍卖，首价密封拍卖

• 在次价密封拍卖中，按照自己的估值出价最优

  一个按照自己估值出价的人不可能通过改变策略得到更大的回报，无论别人出价策略如何。

  因此，我们可以说：“次价支付规则”鼓励真实报价。

• 而首价封闭拍卖中，没有这种性质

10章 匹配市场

• 匹配市场基本模型：二部图

• 匹配市场操作的一般过程：卖方根据买家的需求调整自己的价格

  出价-涨价-出价-涨价…直到买卖双方都满足

  步骤：

  

• 受限组的定义：首先，取二部图右边任何一组节点S，将左边通过边与其相连的节点称为S的邻居，用N(S)表示所有S邻居的集合，如果S比N(S)的数量大，即S比N(S)包含更多的节点，那么右边的S就受到限制

  买方受限组：即在组中，买方的个数多于卖方的个数，需求大于供给

  买方受限组是从买方连到卖方的

• 一定能按照上述步骤得出一个结果

  最终卖方的结果不唯一，但一定是社会最优

11章 中间商市场

• 垄断和竞争：

  

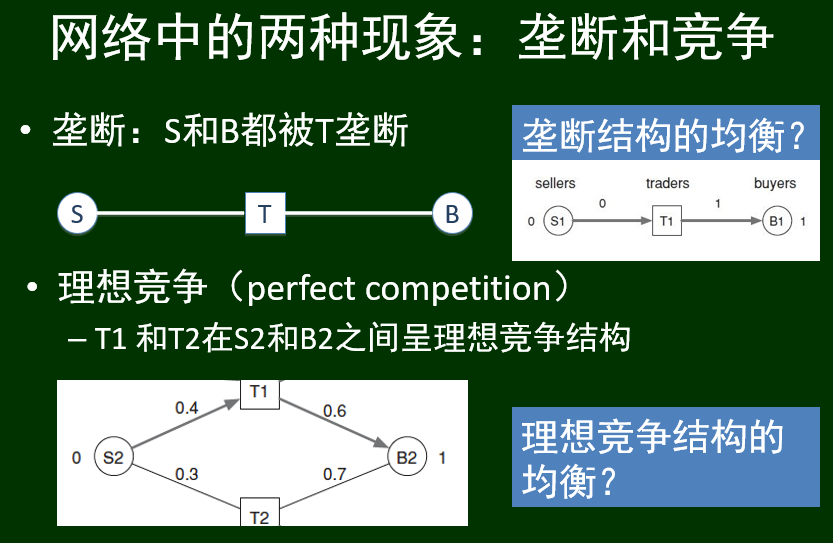
• 社会福利及其最优问题：

  

12章 社交关系价值的均衡

• 定义“结果”：

  

• 稳定结果：

  

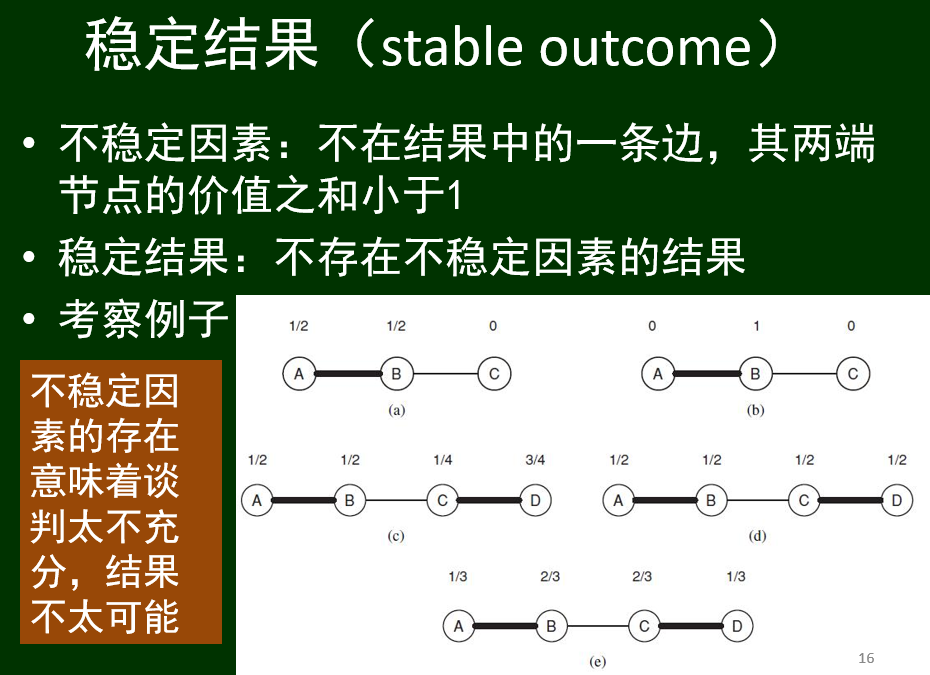
• 平衡结果：

  不稳定因素：不在结果中的一条边，其两端节点的价值之和小于1

  纳什议价解

  

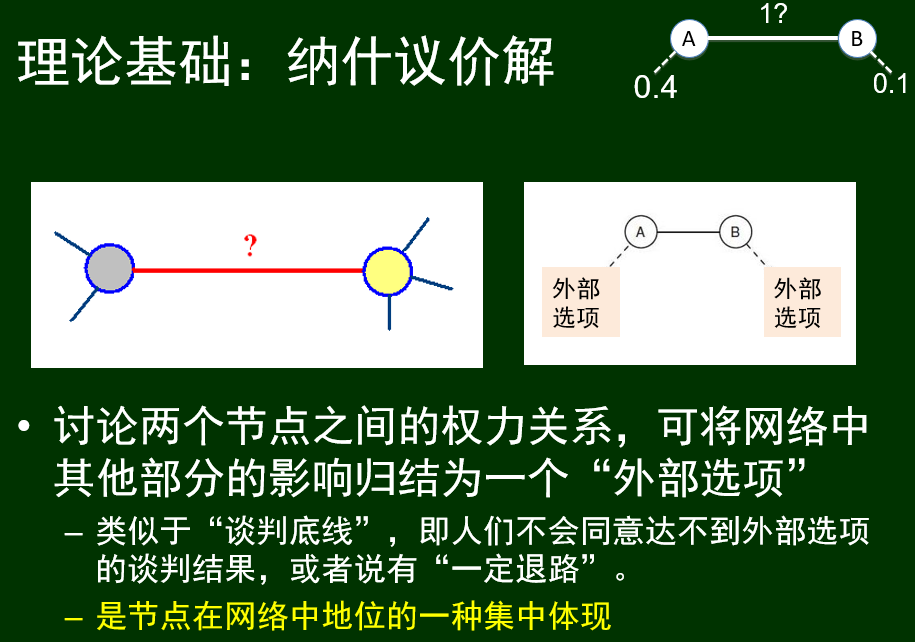
• 外部选项：放弃当前的匹配关系后所能得到的最大好处，即退路的价值

  

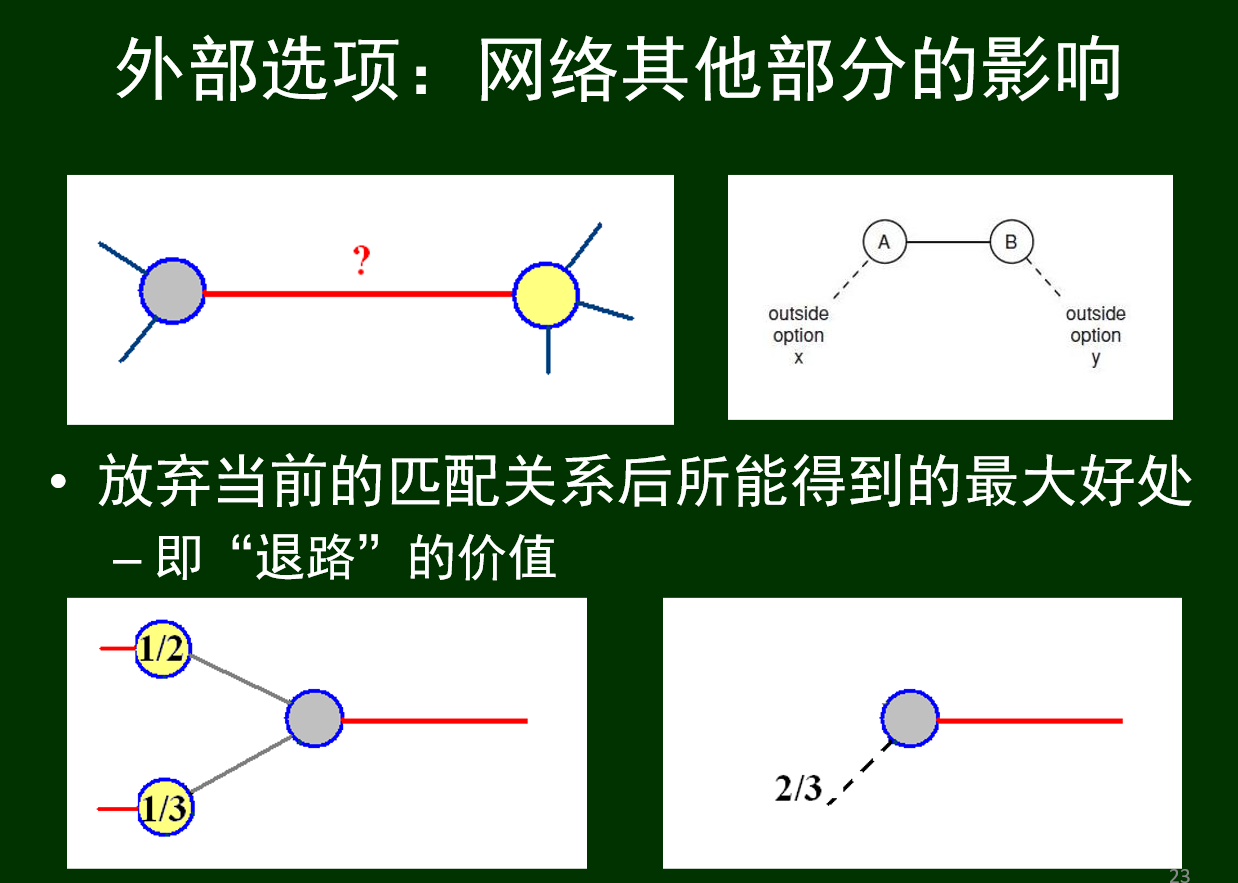
• 平衡结果：（判断结果是否平衡的步骤：求出外部选项->计算结果中每条边的交换是否平衡）

  

• 三个概念的包含关系：【结果【稳定结果【平衡结果】】】

13章 万维网信息的结构

• Web信息结构的模型：

  

• Web信息结构的概貌：

  

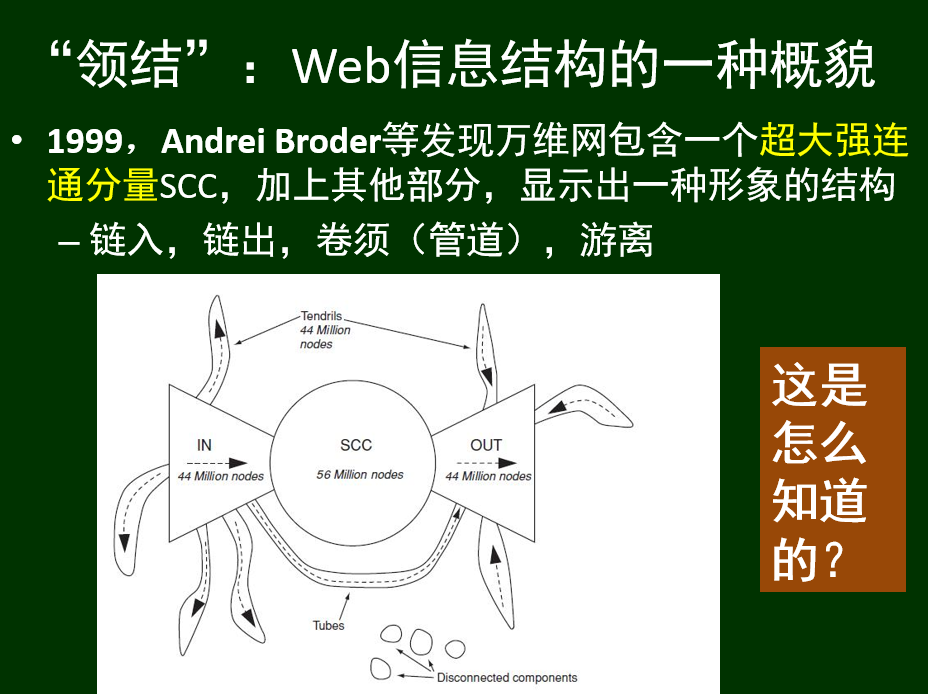
• 给定一个节点，如何确定包含它的强连通分量？

  广度优先搜索（？）

14章 网络信息的链接信息

• 当向搜索引擎中查询一个词时，是什么决定了网页的排名？

  一个网页的链入数越多，排名应该越靠前

  有效利用链接关系蕴含的信息，是搜索引擎超越传统信息检索系统、技术进步的最重要标志

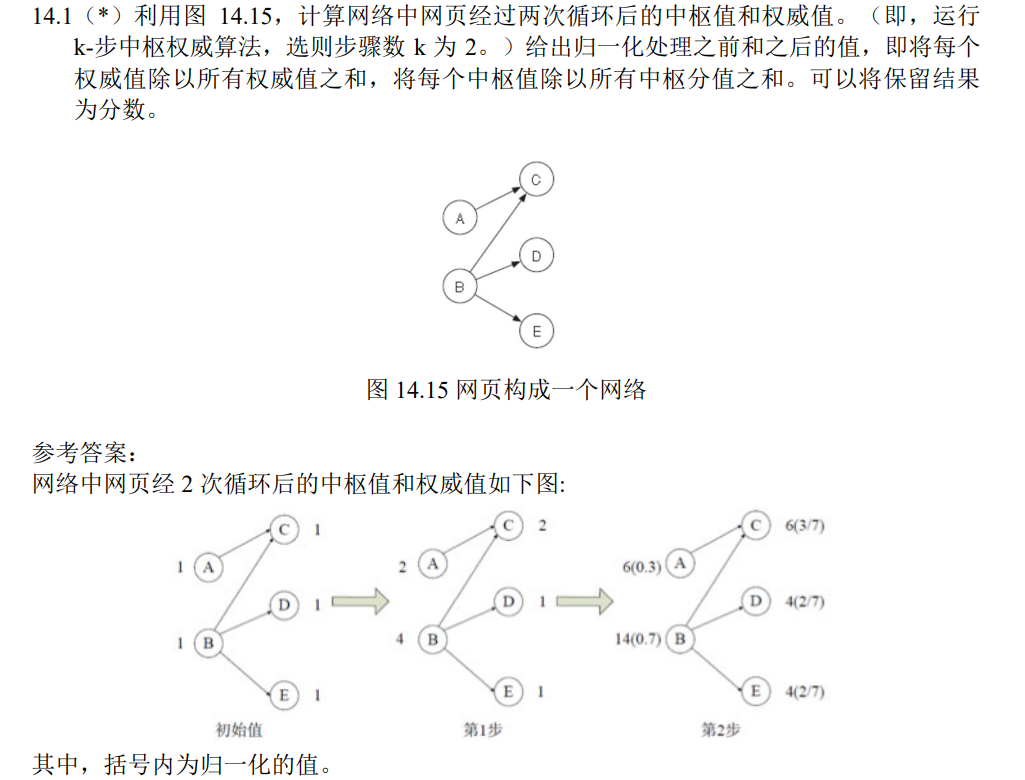
• 网页的中枢性，与权威性

  

  HITS算法：

  权威更新规则：对于每个网页p，以所有指向该网页的网页中枢值之和更新这个网页的权威值

  中枢更新规则：对于每个网页p，以所有该网页指向的网页权威值之和更新这个网页的中枢值

  、

  一个HITS算法的例子：

  先更新权威值，再更新中枢值：

  

• 通过PageRank计算网页的重要性：

  

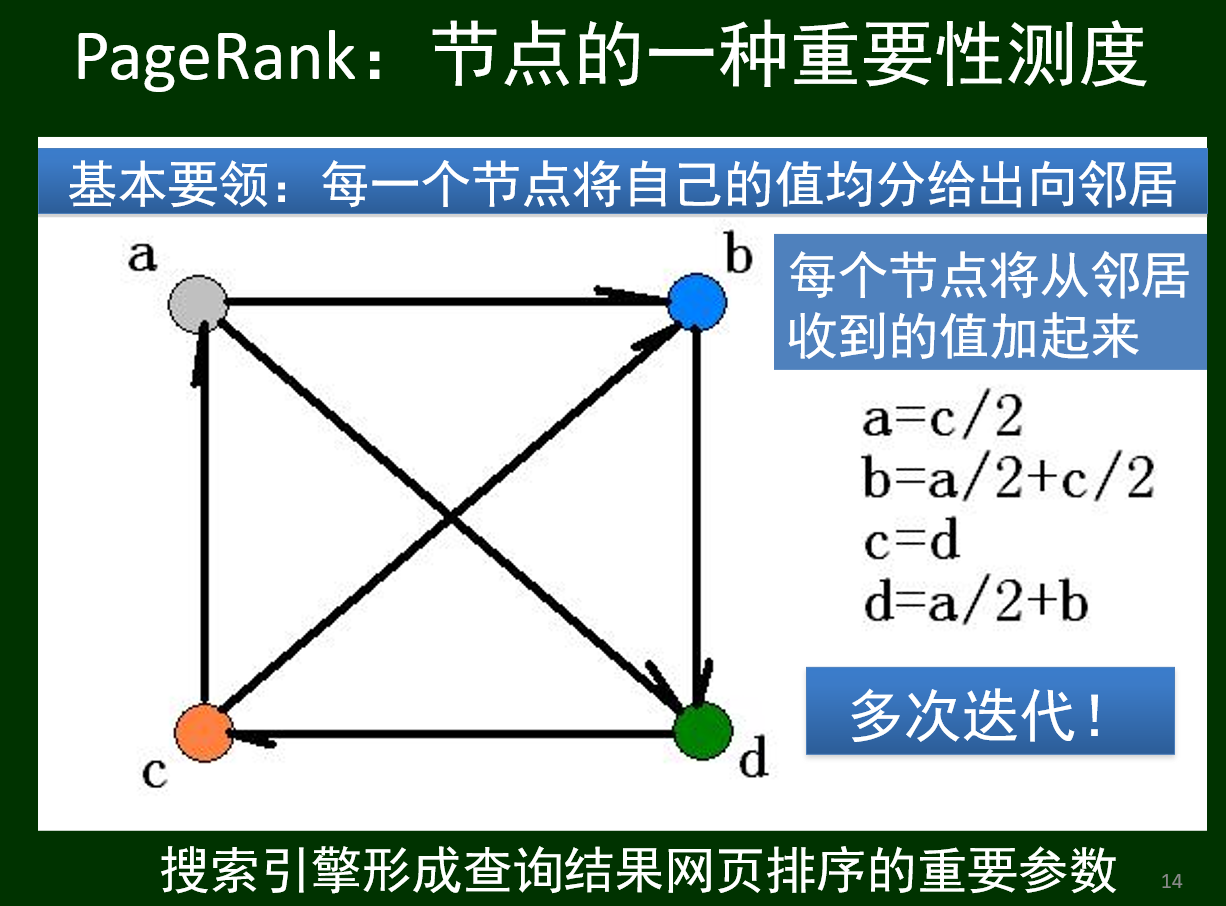
  迭代的例子：

  

  为了避免一些自私的节点只吸收别人的价值，不向外传递，即只被指向，不指向别人，无限次迭代之后

  

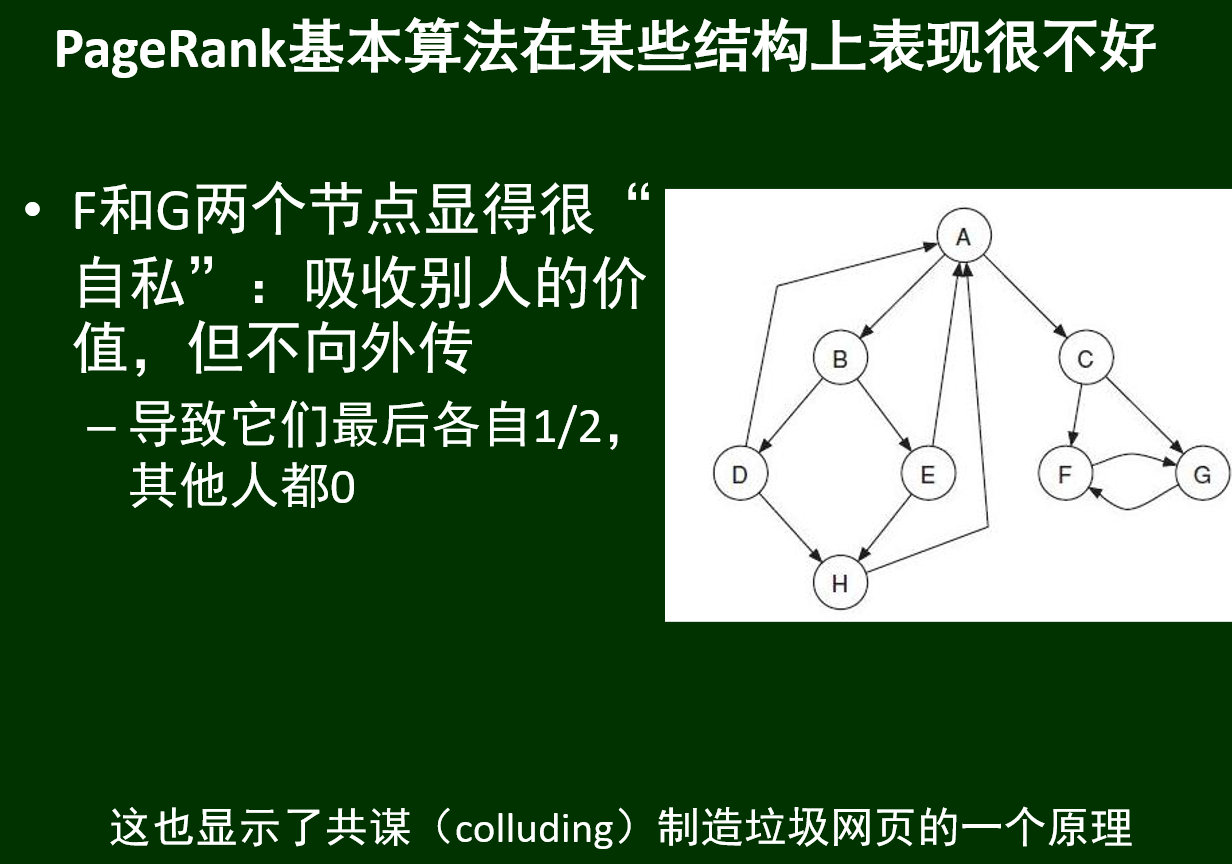
  • 引入同比缩减与统一补偿原则：

    

• 随机游走：PageRank的另一种等价理解：

  

15章 搜索引擎中的广告市场

• 一些概念：

  

  根据点击率和点击收入可以计算出估值，再结合匹配市场中的方法

  

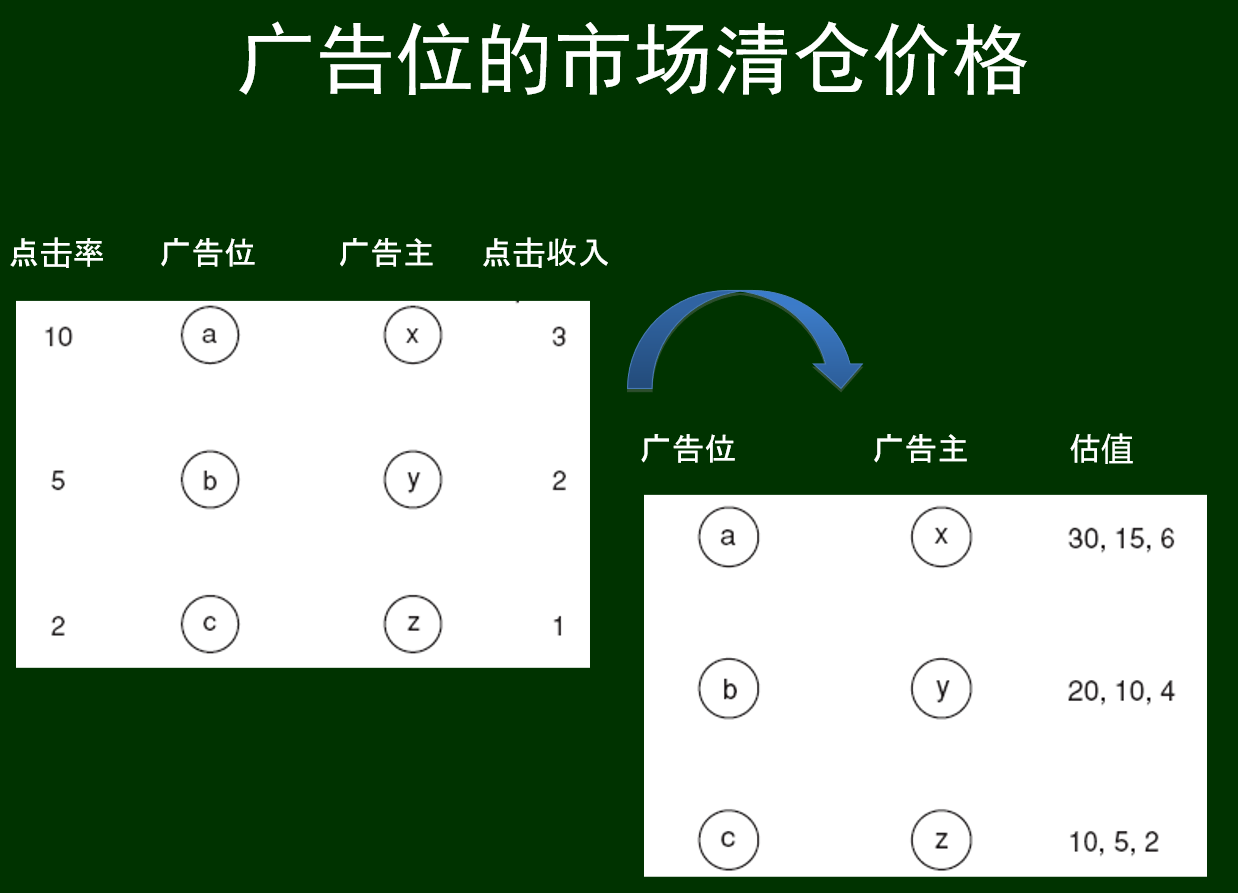
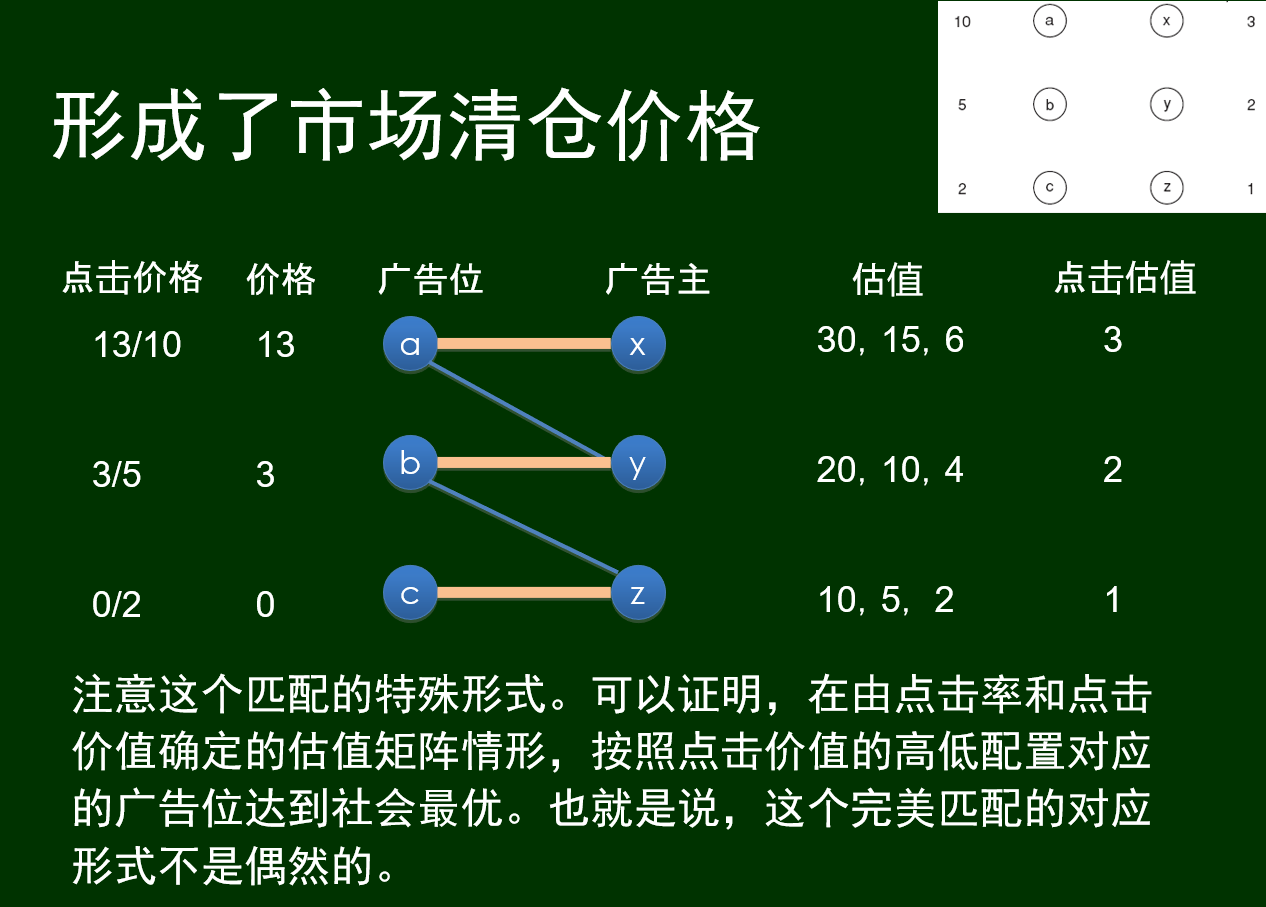
  采用拍卖的方式，GSP：单品次价拍卖机制的一种“自然”推广

  

  在多个商品同时拍卖的情形，如此推广的一种次价拍卖规则（GSP）没有单品次价拍卖（鼓励真实报价）的优良性质

• 改进：

  

  一个例子

  

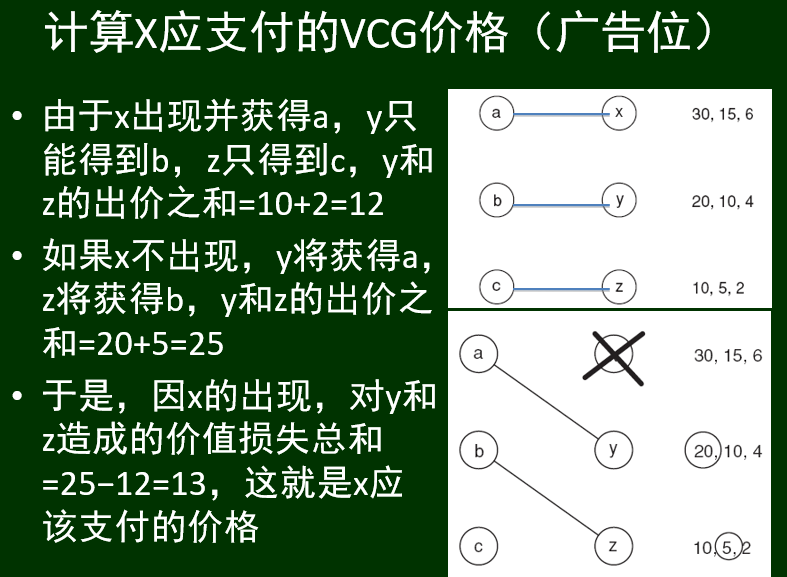
  • 执行步骤

    

• VCG价格机制的优良特性：

  鼓励“讲真话”：按照真实估值出价是每个竞拍者的占优策略

  即没有理由故意让出价偏离估值（无论别人如何出价）

  换言之，大家都按照估值报价是一个纳什均衡

  社会最优：买方估值总和最大

  按照机制执行的定义，当大家都“讲真话”时，所得到的广告位分配就是估值总和最大的

• 但实际中，VCG不好懂，GSP用的更多

18章 幂律与富者更富

• 幂律：流行度的一种主导规律

  图形表示：

  

  幂律的基本特性：

  • 不受观察尺度影响
  • 平均不等于典型
  

  Scale free，意味着从任何一个比例尺度（数据）上看到的函数特征都一样

• “长尾”有利于经营利基产品：除了top-K外，利基产品的总市场占有率随max增加，K是固定的。

  二八定律：“销量排前20%的书的销量之和占总销量的80%”，max增加，比例不变。

20章 小世界现象

• 社会网络中两节点间包含丰富的短路径

  通过“有意识的转发”能够“自动地”找到这些短路径

• 模型推导过程中：

  记 d(v,w) 为v到w的距离（网格步数），则产生一条从v到w的随机边的概率与 d(v,w)^-q^ 成正比

  

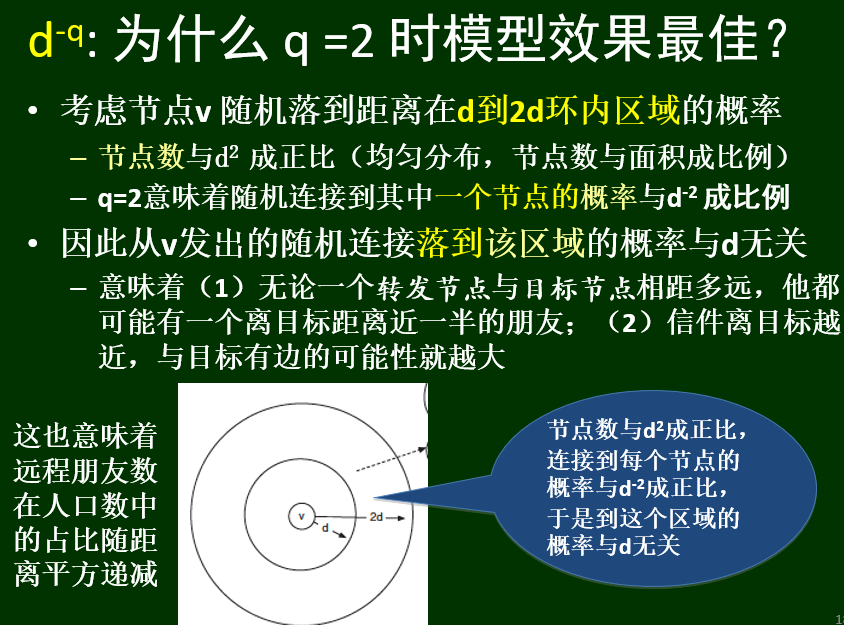
• 但是，在线社会网络如何体现均匀地理位置关系？
  不同节点的同“距离”圈中的节点数相同

  rank的定义：节点w在节点v眼里的排名，rank(w)，等于网络中比w离v近的节点的个数

  把社会网络中的rank与地理距离中的d^2^类比

  rank小的在圆内==面积小的在圆内

  

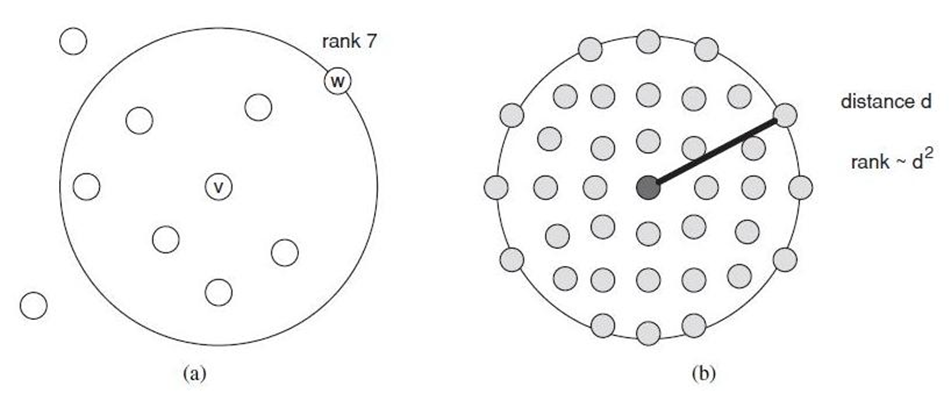
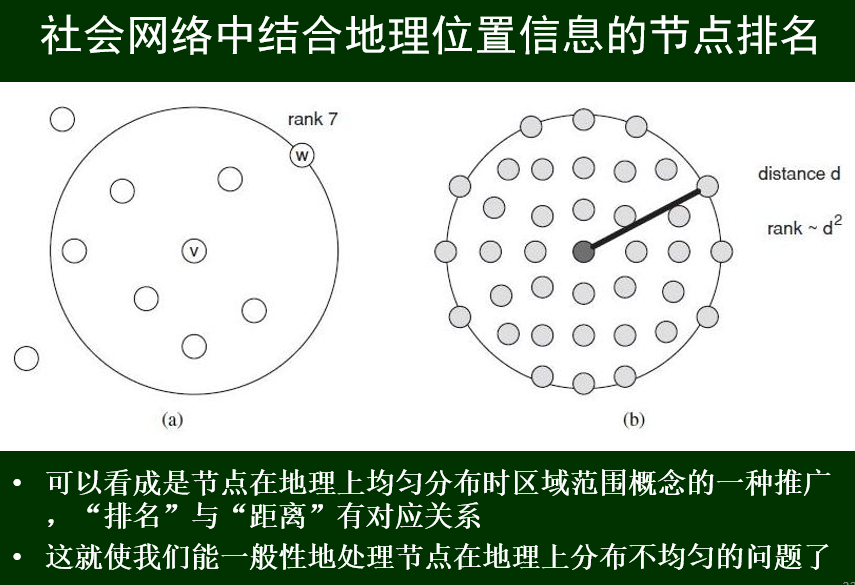
• 互联网的地域性——虚拟空间距离与现实空间距离的等价性

  远程相邻节点的数量在同距离节点数中的占比随距离的平方减少

• 另一个社会网络中的距离概念：社会距离

  

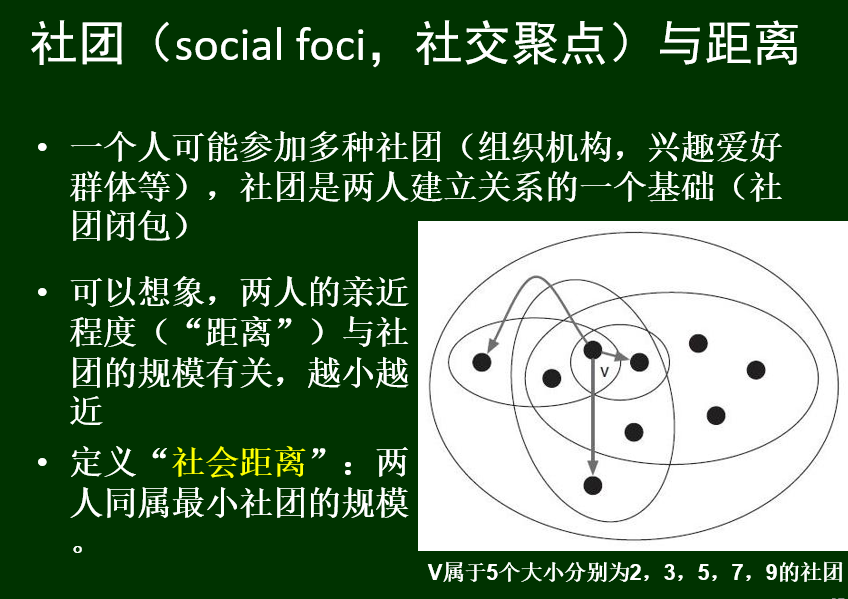
21章 传染病的网络宣传模型

树形模型（分支结构），SIR模型

• 基本再生数：R0=概率p×遇到的人数k，由单一个体引起的新发病例数期望值

  如果R0<1，则疾病将以概率1在有限的过程后消失。如果 R0> 1，则疾病持续在每一波以一定的概率至少感染一个人

  

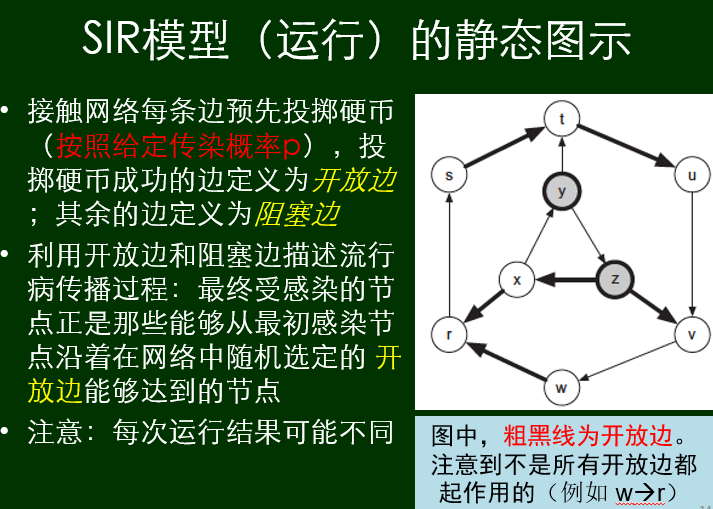
• SIR模型

  

  与分支结构不同，这里不再有k这个参数。而是靠网络结构和时间步数来表达传染的过程。

  一条边表示，“在特定的时候，他们有接触”

  

手写的笔记

• 本文作者：wan_nan
• 本文链接：https://wan-nan.github.io/2022/04/26/%E7%A4%BE%E4%BC%9A%E7%BD%91%E7%BB%9C%E5%A4%8D%E4%B9%A0/
• 版权声明：本博客所有文章除特别声明外，均默认采用 许可协议。