第一章 性能
计算Amdahl定律和CPU时间时要将各个量都算清楚!!
- 以经常性事件为重点
- Amdahl定律
- CPU性能公式
- 程序的局部性原理
- MIPS和程序执行时间Te
Amdahl定律
系统性能加速比:

加速比依赖于两个因素:
(两个因素都是用比例描述的)

改进后的总执行时间**Tn和系统加速比Sn**如下:

Sn、T0、Tn知二求一
Amdahl定律:一种性能改进的递减规则

CPU性能公式
CPU时间 = IC ×CPI ×时钟周期时间
- IC:所执行的指令条数
- CPI:每条指令执行的平均时钟周期数(Cycles Per Instruction)
- 时钟周期时间是系统时钟频率的倒数


MIPS/Te

例题
例1.4:
要额外考虑的问题是:CPU2的程序量为CPU1的
70%,不能仅仅以比例的视角看CPU时间
1.10


第三章 流水线
时空图
通过时间和排空时间见下图所示
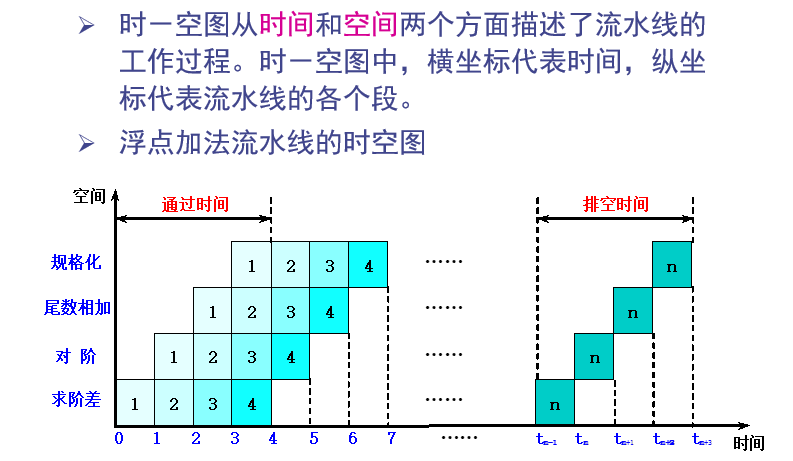
- 流水线中时间最长的段将成为流水线的瓶颈
流水线分类
按照流水技术用于计算机系统的等级不同
部件级流水线(运算操作流水线)
例如流水线分为:浮点加法,求阶差,对阶,尾数相加,规格化几个阶段时
按照运算操作的类型进行阶段划分
处理机级流水线(指令流水线)
例如:取址,译码,执行,访存,写回
把一条指令的执行过程分解为若干个子过程,每个子过程在独立的功能 部件中执行
系统级流水线(宏流水线)
把多台处理机串行连接起来,对同一数据流进行处理,每个处理机完成整个任务中的一部分
按照流水线所完成的功能来分类
- 单功能流水线:只能完成一种固定功能的流水线。
- 多功能流水线:流水线的各段可以进行不同的连接,以实现不同的功能。
按照同一时间内各段之间的连接方式对多功能流水线作进一步的分类
- 静态流水线:在同一时间内,多功能流水线中的各段只能按同一种功能的连接方式工作
- 动态流水线:在同一时间内,多功能流水线中的各段可以按照不同的方式连接,同时执行多种功能
静态流水线:排空后,才可执行其他功能
动态流水线:不同功能可同时在流水线中执行
按照流水线中是否有反馈回路来进行分类
- 线性流水线:流水线的各段串行连接,没有反馈回路。数据通过流水线中的各段时,每一个段最多只流过一次
- 非线性流水线:流水线中除了有串行的连接外,还有反馈回路
非线性流水线的调度问题:确定什么时候向流水线引进新的任务,才能使该任务不会与先前进入流水线的任务发生冲突——争用流水段
根据任务流入和流出的顺序是否相同来进行分类
顺序流水线:流水线输出端任务流出的顺序与输入端任务流入的顺序完全相同。每一个任务在流水线的各段中是一个跟着一个顺序流动的
例如经典的五段指令流水线
乱序流水线:流水线输出端任务流出的顺序与输入端任务流入的顺序可以不同,允许后进入流水线的任务先完成(从输出端流出)。也称为无序流水线、错序流水线、异步流水线
当今的指令流水线都是乱序流水线
标量处理机与向量流水处理机

流水线的性能指标
吞吐率、加速比、效率
吞吐率:

各段时间均相等的流水线
n是任务数,k是流水线段数
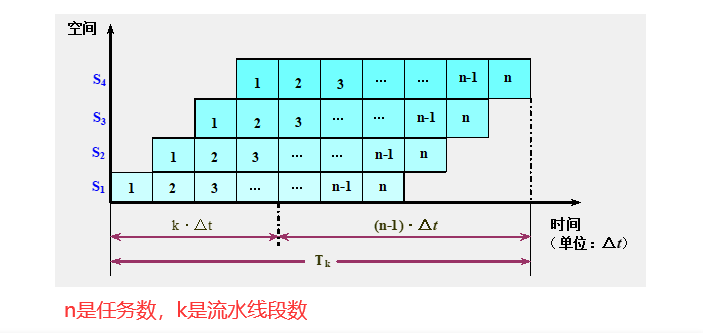
实际吞吐率和最大吞吐率
当n>>k,即任务数量远远大于流水线段数时,流水线吞吐率最大

各段时间不完全相等的流水线
吞吐率计算用时空图或下面的公式

解决流水线瓶颈问题常用方法:
细分瓶颈段
将$3\Delta t$的一段分为三个$\Delta t$的段
重新设置瓶颈段(使用并行部件,增加硬件成本)
如下图所示:设置三段$S_4$,轮流使用,提高了硬件开销
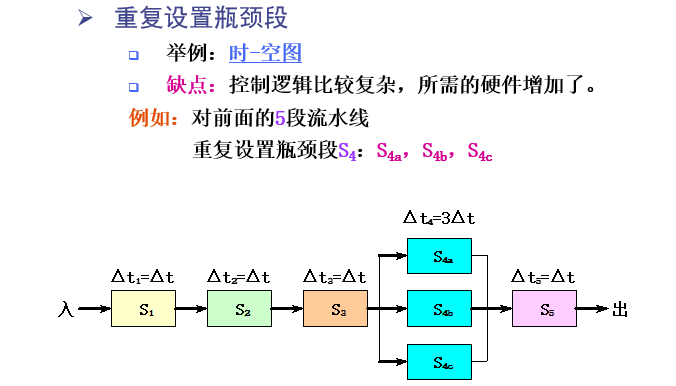
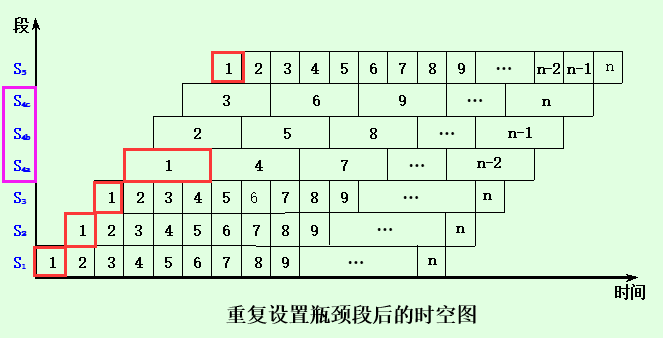
加速比:
完成同样一批任务,不使用流水线所用的时间与使用流水线所用的时间之比。
流水线各段时间相等(都是$\Delta t$)

当n>>k时,加速比取到最大,为k
k是流水线的段数,所以流水线段数越多,加速比越大
流水线的各段时间不完全相等时
总之记住k段流水线完成n个任务耗时

流水线的效率:
流水线中的设备实际使用时间与整个运行时间的比值,即流水线设备的利用率
各段时间相等时,各段的效率相同,均为$e=\frac{n\Delta t}{T_k}=\frac{n}{k+n-1}$
整条流水线的效率为各段效率的平均,在$n>>k$时流水线总效率最大,取到1
几个量的关系:

从时空图上看,效率就是n个任务占用的时空面积和k个段总的时空面积之比
题目
分析流水线性能
静态流水线
时空图要画对
读题:静态流水线or动态流水线
静态流水线:排空后,才可执行其他功能
动态流水线:不同功能可同时在流水线中执行
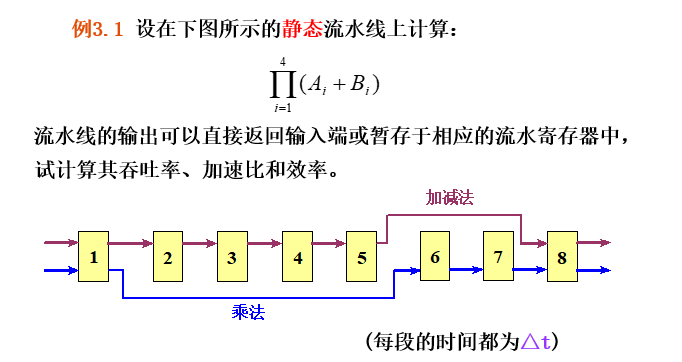
步骤:
- 选择适合于流水线工作的算法
- 画出时空图
- 计算性能
答案:
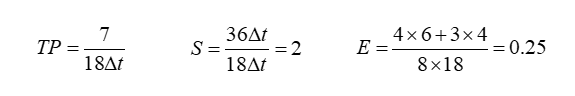
动态流水线
不同功能可同时在流水线中执行,加和乘可以无缝切换,不用排空流水线
非线性流水线的调度
冲突向量右移$j$位后和最开始的冲突向量C0取或运算
$j$取自禁止表
启动距离:向一条非线性流水线的输入端连续输入两个任务之间的时间间隔称为非线性流水线的启动距离
禁用启动距离:会引起非线性流水线功能段使用冲突的启动距离则称为禁用启动距离
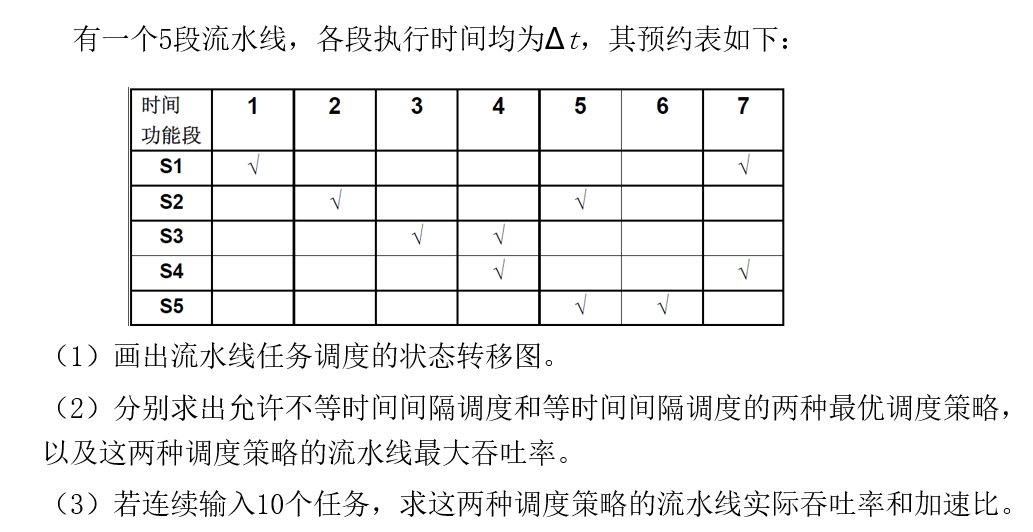
预约表
横向(向右):时间(一般用时钟周期表示)
纵向(向下):流水线的段
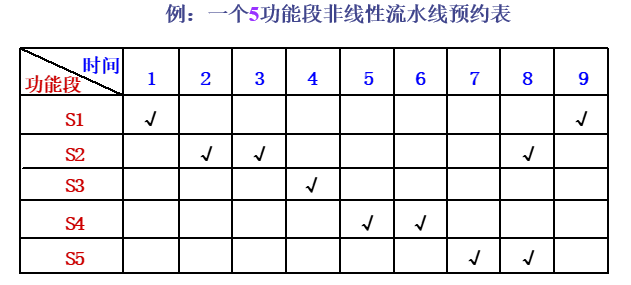
根据预约表写出禁止表F
上图中禁止表:

对于禁止表F= { 1,5,6,8 }
,其冲突向量为C0=(10110001)冲突向量:
注意从右往左数,从1到N

冲突向量右移$j$位后和最开始的冲突向量C
0取或运算$j$取自禁止表
状态转移图:
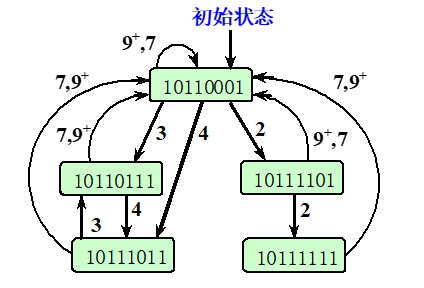
每个状态引出的线都应该包括其自身禁止表中的所有值,以及9^+^(长度为8,则取9^+^,表示间隔时间大于预约表的最长时间)
由初始状态出发,任何一个闭合回路即为一种调度方案。


流水线的相关与冲突
RISC流水线
经典的5段RISC流水线
取指(IF)
- 以程序计数器PC中的内容作为地址,从存储器中取出指令并放入指令寄存器IR;
- 同时PC值加4(假设每条指令占4个字节),指向顺序的下一条指令。
译码/读寄存器(ID)
- 对指令进行译码,并用IR中的寄存器地址去访问通用寄存器组,读出所需的操作数。
执行/有效地址计算周期(EX)
寄存器中的值在译码阶段就已经取出来了
不同指令所进行的操作不同
- load和store指令:ALU把指令中所指定的寄存器的内容与偏移量相加,形成访存有效地址。
- 寄存器-寄存器ALU指令:ALU按照操作码指定的操作对从通用寄存器组中读出的数据进行运算。
- 寄存器-立即数ALU指令:ALU按照操作码指定的操作对从通用寄存器组中读出的操作数和指令中给出的立即数进行运算。
- 分支指令:ALU把指令中给出的偏移量与PC值相加,形成转移目标的地址。同时,对在前一个周期读出的操作数进行判断,确定分支是否成功。
存储器访问/分支完成周期(MEM)
该周期处理的指令只有load、store和分支指令。其它类型的指令在此周期不做任何操作。
load指令:用上一个周期计算出的有效地址从存储器中读出相应的数据;
store指令:把指定的数据写入这个有效地址所指出的存储器单元。分支指令:
分支“成功”,就把转移目标地址送入PC。分支指令执行完成。
写回周期(WB)
ALU运算指令和load指令在这个周期把结果数据写入通用寄存器组。
这种实现方案中各个指令的耗时:

相关
相关有三种类型:数据相关(真数据相关)、名相关、控制相关
数据相关:
注意指令操作数的位置

名相关:
如果两条指令使用相同的名,但是它们之间并没有数据流动,则称这两条指令存在名相关。
- 反相关:指令j写的名=指令i读的名
- 输出相关:指令j写的名=指令i写的名
控制相关:
控制相关是指由分支指令引起的相关
流水线冲突
三种类型:
结构冲突、数据冲突、控制冲突
如果某种指令组合因为资源冲突而不能正常执行,则称该处理机有结构冲突。
例如访存冲突
数据冲突:
三种冲突:
- 写后读冲突,对应真数据相关
- 写后写冲突:对应输出相关
- 读后写冲突:对应反相关
定向
通过定向技术减少数据冲突引起的停顿

并不是所有的数据冲突都可以通过定向技术解决
无法将LD指令(Load)的结果定向到DADD指令
需要插入一个气泡
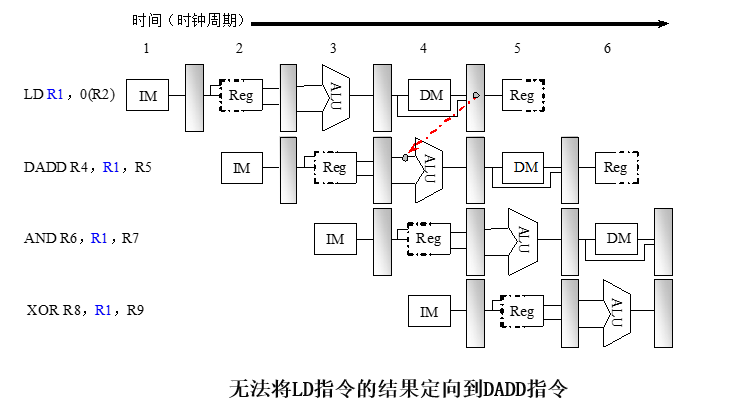
依靠编译器解决数据冲突
让编译器重新组织指令顺序来消除冲突,这种技术
称为指令调度或流水线调度。指令调度举例:

控制冲突 分支相关
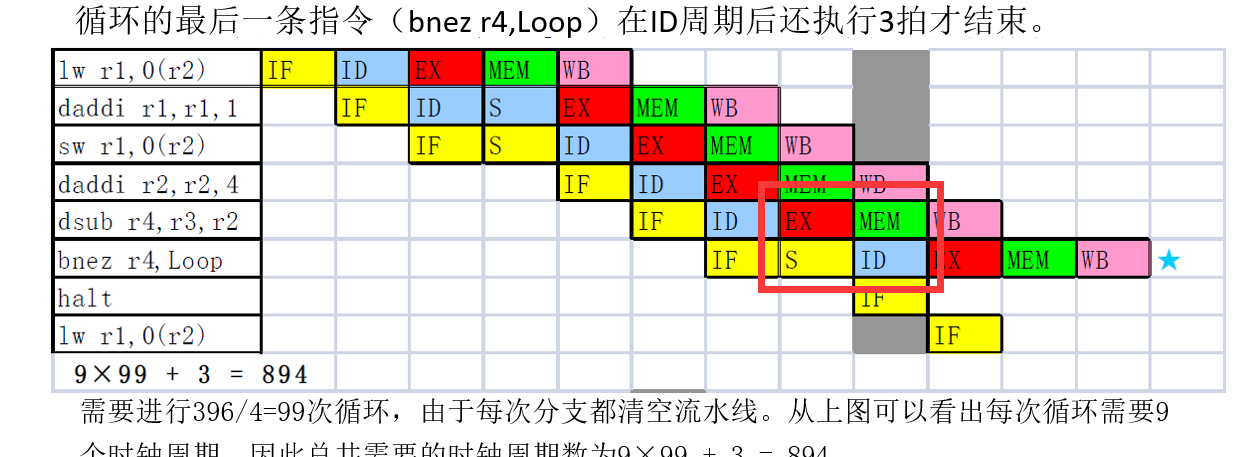
简单处理分支指令:分支成功的情况
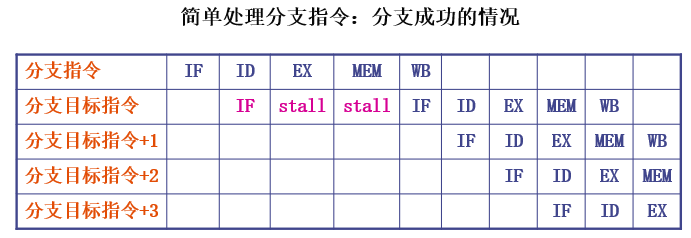
等分支地址在MEM阶段计算完毕后,目标指令的IF阶段才能开始
这个例子中分支延迟为3
可以采取两种措施来减少分支延迟
- 在流水线中尽早判断出分支转移是否成功
- 尽早计算出分支目标地址
通过将【判断分支是否成功】和【分支目标地址的计算】两步提前到ID段完成,分支延迟可以被降低为1个时钟周期
流水线对分支的处理:
预测不跳转
允许分支指令后的指令继续在流水线中流动,就好像什么都没发生似的
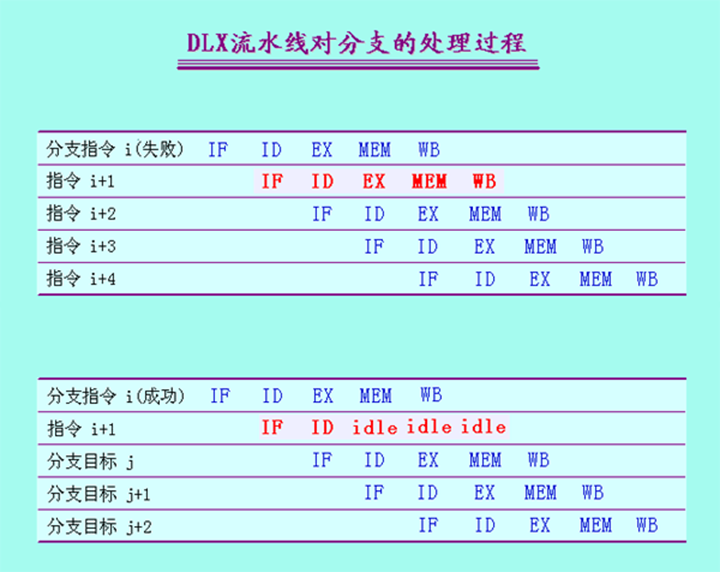
预测跳转
延迟分支(延迟槽)
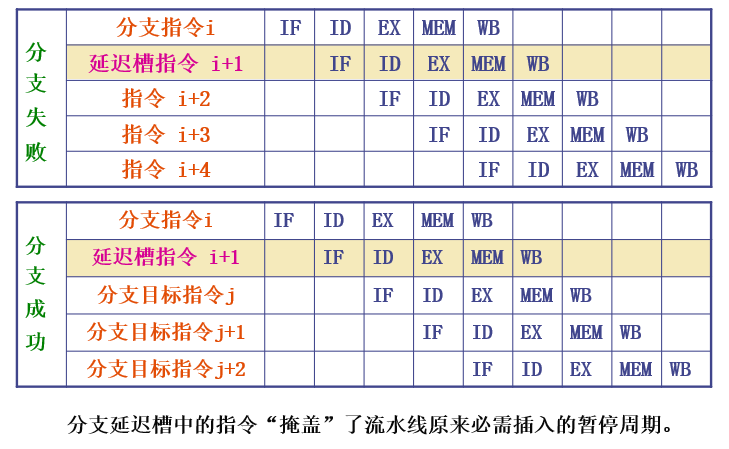
三种调度方法:
- 从前调度
- 从目标处调度
- 从失败处调度
作业题
3.10
最后要排空流水线,最后一个任务耗时为$7\Delta t$

3.11
注意读题
在一个时钟周期中对同一个寄存器的读操作和写操作可以通过寄存器“定向”

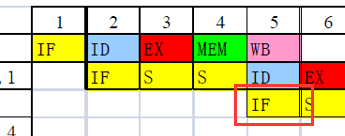
上面在3和4时刻插入两个气泡,
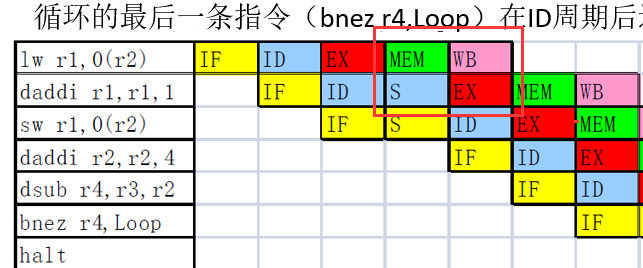
load-use问题上一个指令是load指令,结果需要在MEM阶段结束才能得到,那么下一条指令要想在EX阶段获取操作数,就要插入一个气泡
流水线插入气泡是同时全部阶段一起插入的,所以第二条和第三条指令插入气泡的时刻一样
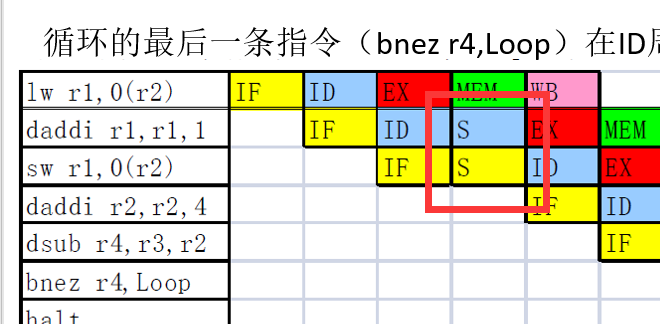
想象流水寄存器的存在,上一条指令的结果在EX阶段得出
如果是普通使用ALU的非分支指令,可以通过定向技术,直接将上一条指令ALU的结果定向到下一条指令的ALU的输入,避免插入气泡
如下图:
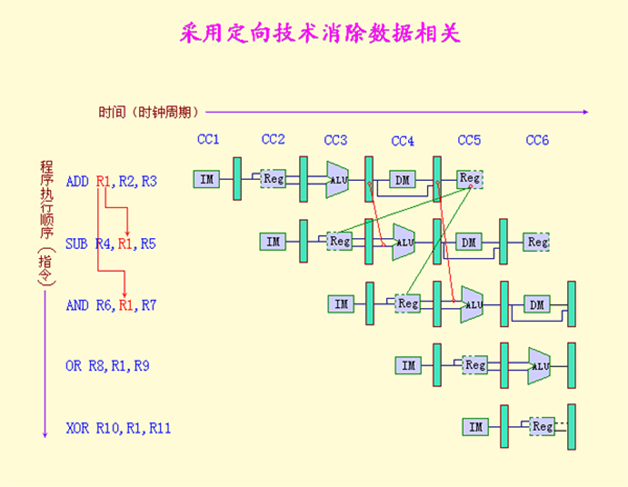
但分支指令需要在ID段就确定是否跳转以及跳转目标地址
那么需要插入一个气泡,等上一个指令在EX段将结果计算出后再【定向】到下一条指令的ID段
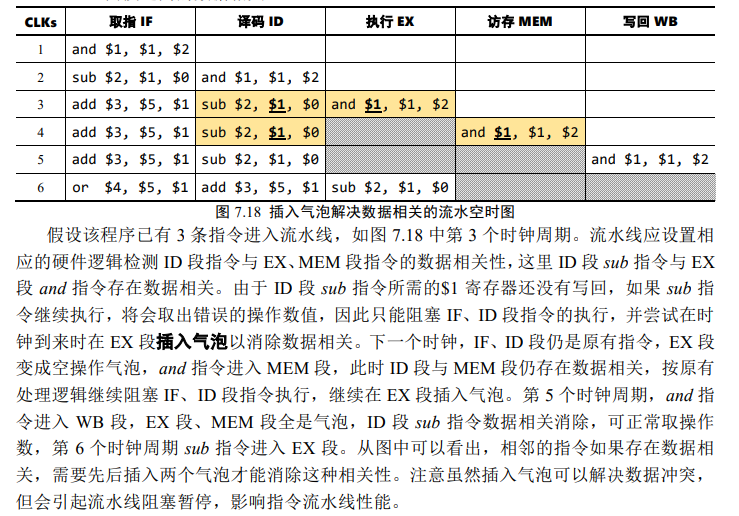
如果没有定向技术在,则要按照下面的情况考虑
ID和EX冲突:插入一个气泡,编程ID和MEM冲突(一共需要两个气泡)
ID和MEM冲突:插入一个气泡
ID和WB冲突:通过先写后读,寄存器堆写入控制采用下跳沿触发,而所有流水寄存器采用上跳沿触发,来解决
预测分支失败:(即预测不跳转,顺序取指令)
- 若确定分支失败,将分支指令看作是一条普通指令,流水线正常流动
- 若确定分支成功,流水线就把在分支指令之后取出的所有指令转化为空操作,并按分支目地
重新取指令执行
预测分支成功:(即预测会跳转)
- 但是在前述5段流水线中,这种方法没有意义,因为还是要在ID段结束才能知道跳转地址,才能获取分支目标地址的指令,还是会暂停一个周期
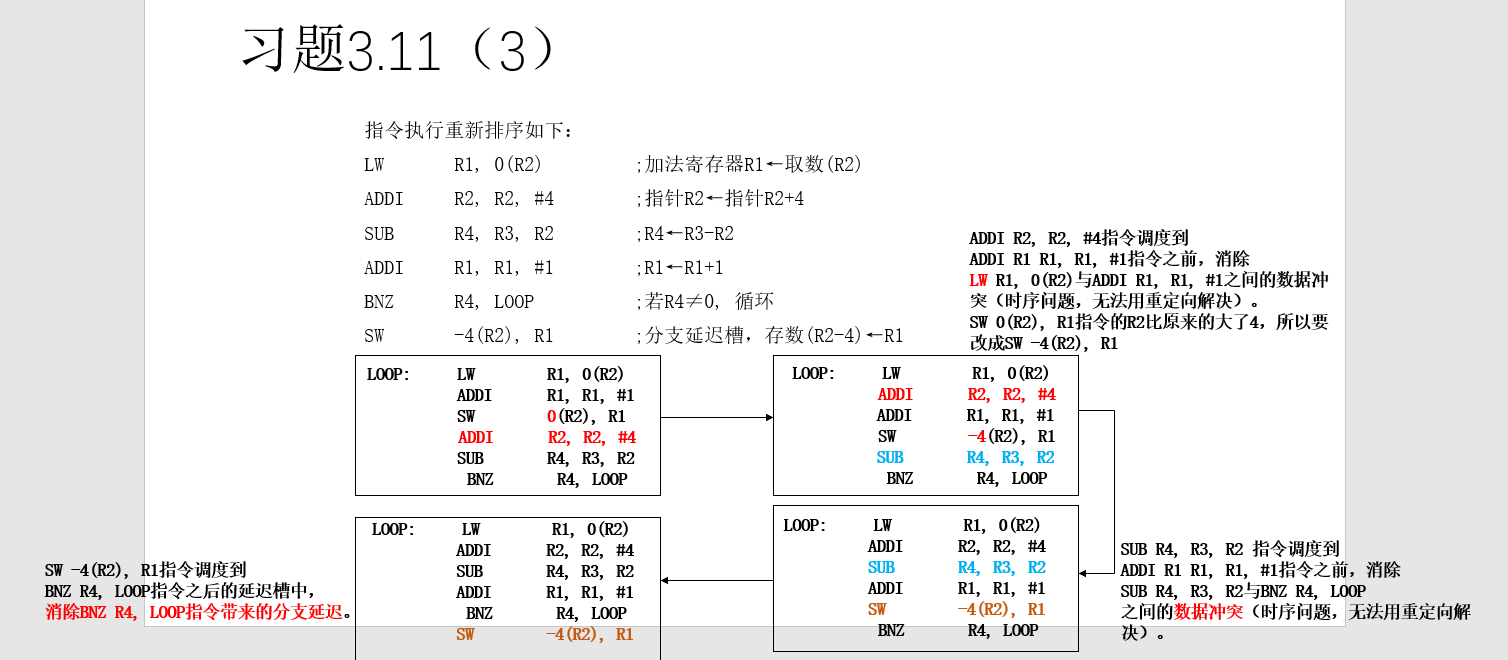
3个点:
load-use问题:要避免在load指令下面相邻就出现数据冲突
(控制相关)分支指令问题:避免分支指令上面相邻就出现数据冲突
分支延迟问题:避免将分支指令放在最后一个,要在分支指令后面插入一条指令以避免分支延迟
第五章 指令级并行
动态分支预测
动态分支预测:
动态分支预测:在程序运行时,根据分支指令过去的表现来预测其将来的行为。
如果分支行为发生了变化,预测结果也跟着改变。
有更好的预测准确度和适应性。采用动态分支预测的目的:
预测分支是否成功
尽快找到分支目标地址(或指令)
(避免控制相关造成流水线停顿)
分支历史表BHT是最简单的动态分支预测方法
其只有在这样的情况下才有用:判定分支是否成功所需的时间大于确定分支目标地址所需的时间
5段经典流水线中BHT没好处
分支目标缓冲器BTB
将分支成功的分支指令的地址和它的分支目标地址都放到一个缓冲区中保存起来,缓冲区以分支指令的地址作为标识
BTB的执行流程:
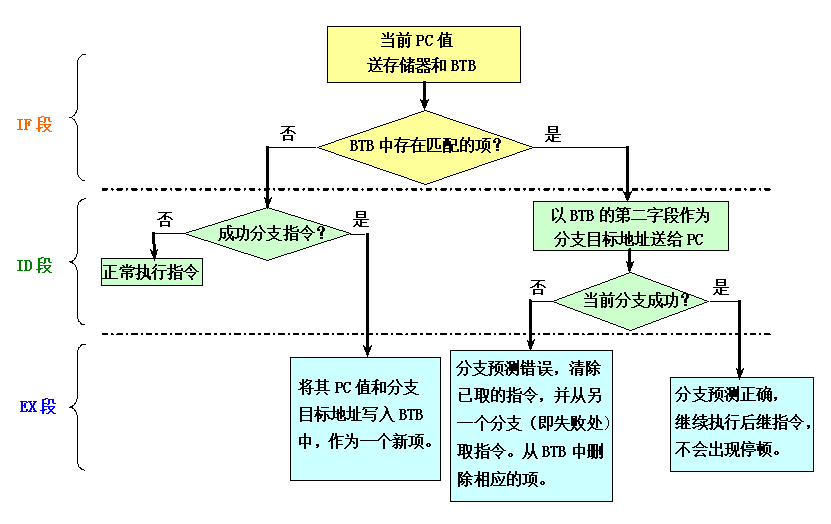
开销:
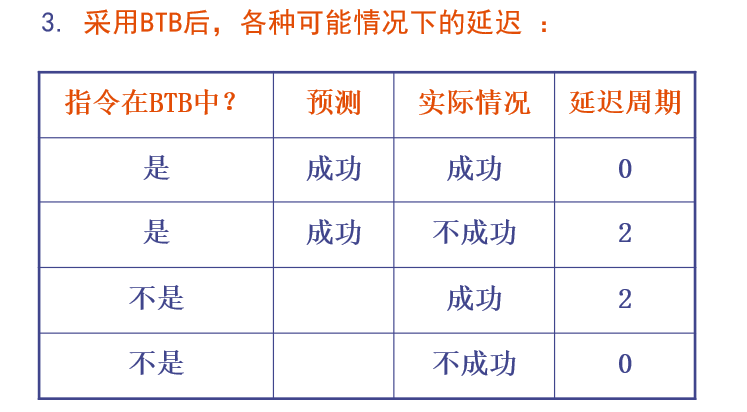
可以改进
增加两位的BHT
存分支目标处的指令,而非分支目标地址
因为IF是通过指令地址取指令,分支成功,程序的空间局部性被破坏,取指令的时延很可能会增加(1级i-cache miss)
多指令流出技术
三种:
超长指令字、超标量、超流水处理机
要会画各自的流水时空图
看例题5.11就够了
实际CPI = 理想CPI==+==各种停顿拍数
前面的动态分支预测技术是在试图降低后者,即各种分支指令的停顿拍数
而可以通过在每个时钟周期内流出多条指令, 使CPI<1,来降低前者,理想CPI
多流出处理机有两种风格:

基于静态调度的多流出技术
假设:每个时钟周期流出两条指令:1条整数型指令+1条浮点操作指令
其中:把load指令、store指令、分支指令归类为整数型指令。
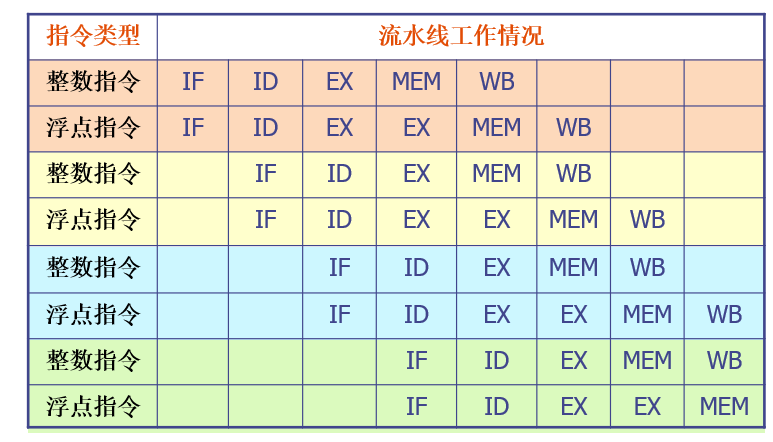
限制其性能发挥的障碍

超流水处理机
对于一台每个时钟周期能流出n条指令的超流水线计算机来说,这n条指令不是同时流出的,而是每隔1/n个时钟周期流出一条指令。
实际上该超流水线计算机的流水线周期为1/n个时钟周期。
一台每个时钟周期分时流出两条指令的超流水线计算机的时空图
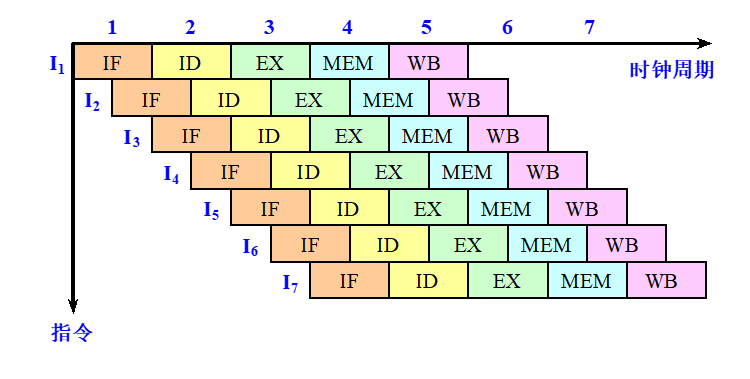
题目
5.8
程序执行的CPI=没有分支的基本CPI+分支带来的额外开销
上述两个开销直接相加
命中率为90%,则有10%的几率未命中,开销为3
预测精度90%,则有**90%×10%**的几率命中并预测错误,开销为4

5.9
实际CPI = 理想CPI==+==各种停顿拍数【加!】

5.11
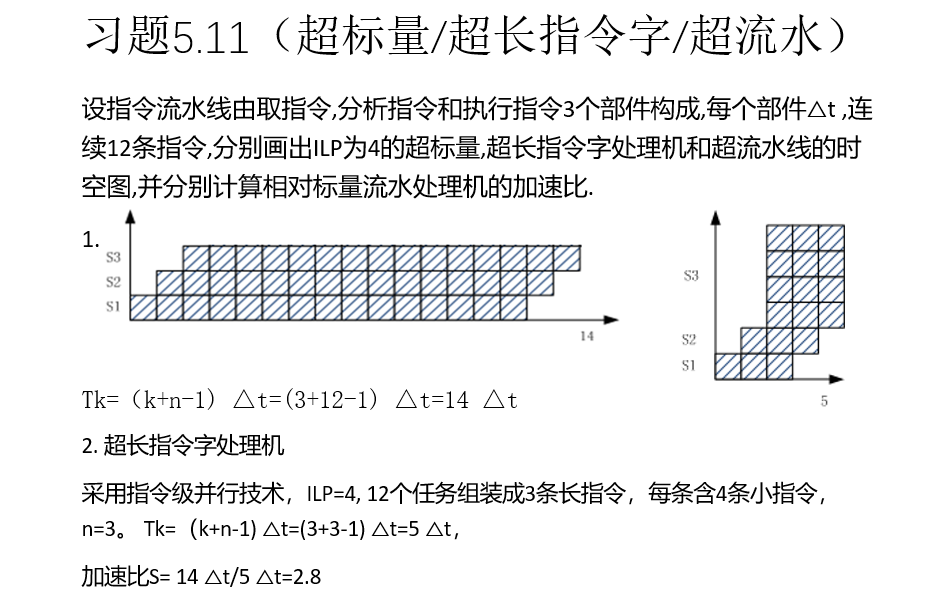
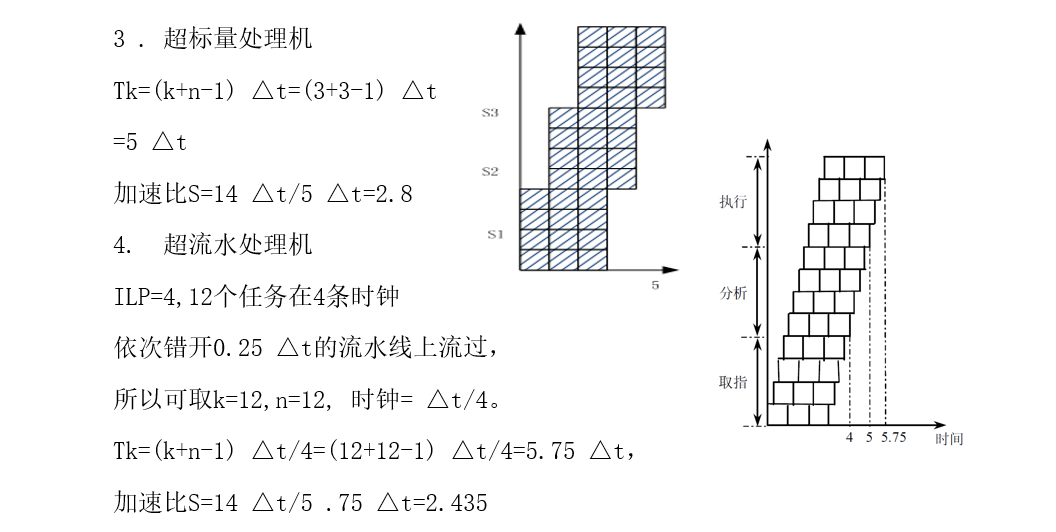
第七章 存储系统
存储系统性能指标
访问时间T、容量S、平均每位价格C
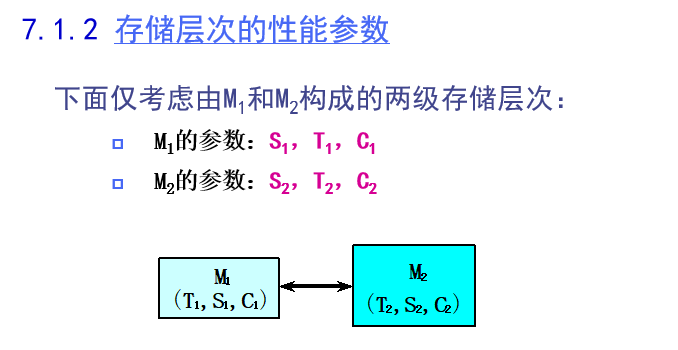
整体的存储容量、每位价格、命中率、平均访问时间

命中率的定义:CPU访问存储系统时,在M1中找到所需信息的概率


先访问小的M1,再访问大的M2
$$
T_A:平均访问时间\
不命中开销T_M:从向M_2发出访问请求到把整个数据块调入M_1中所需的时间\
T_A = T_1+F·T_M\
T_M=T_2+T_B\
T_B:传送一个信息块所需的时间
$$
Cache基本知识
Cache基本工作原理
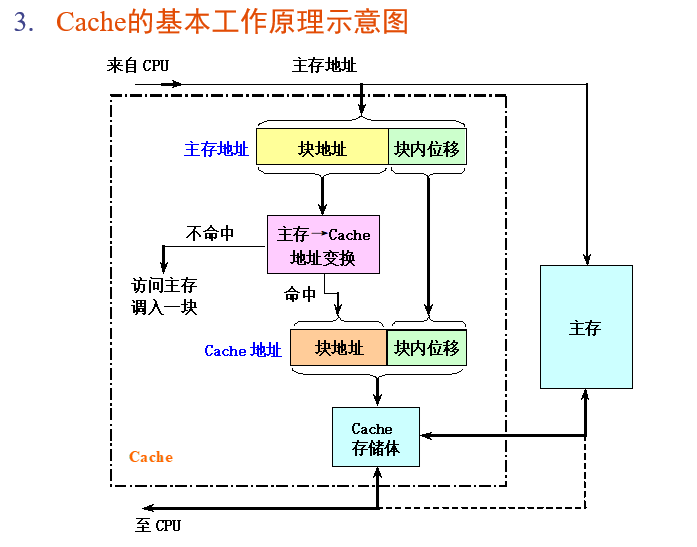
映象规则
全相联:

直接相联:


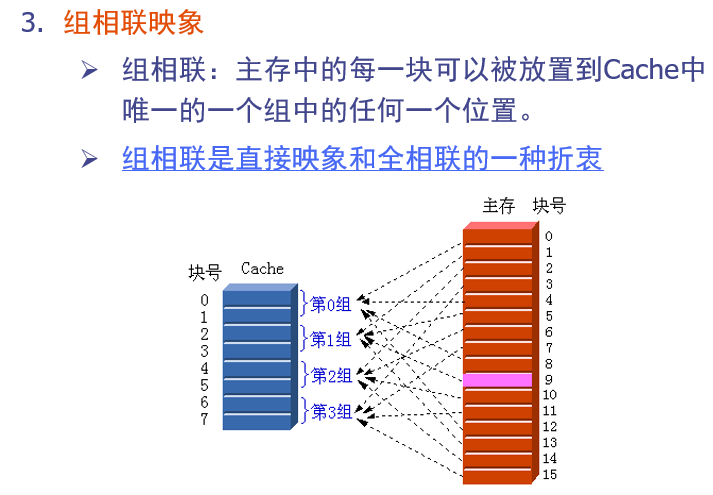
组相联:
“组”是Cache的概念
n 路组相联:每组中有n个块 ( n=M/G )

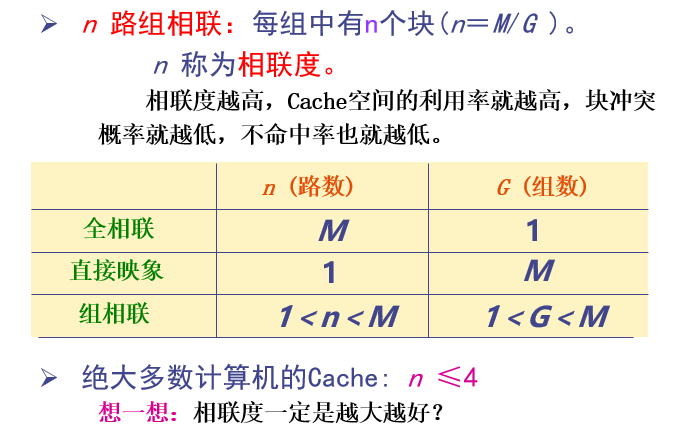
查找方法
我跳过了
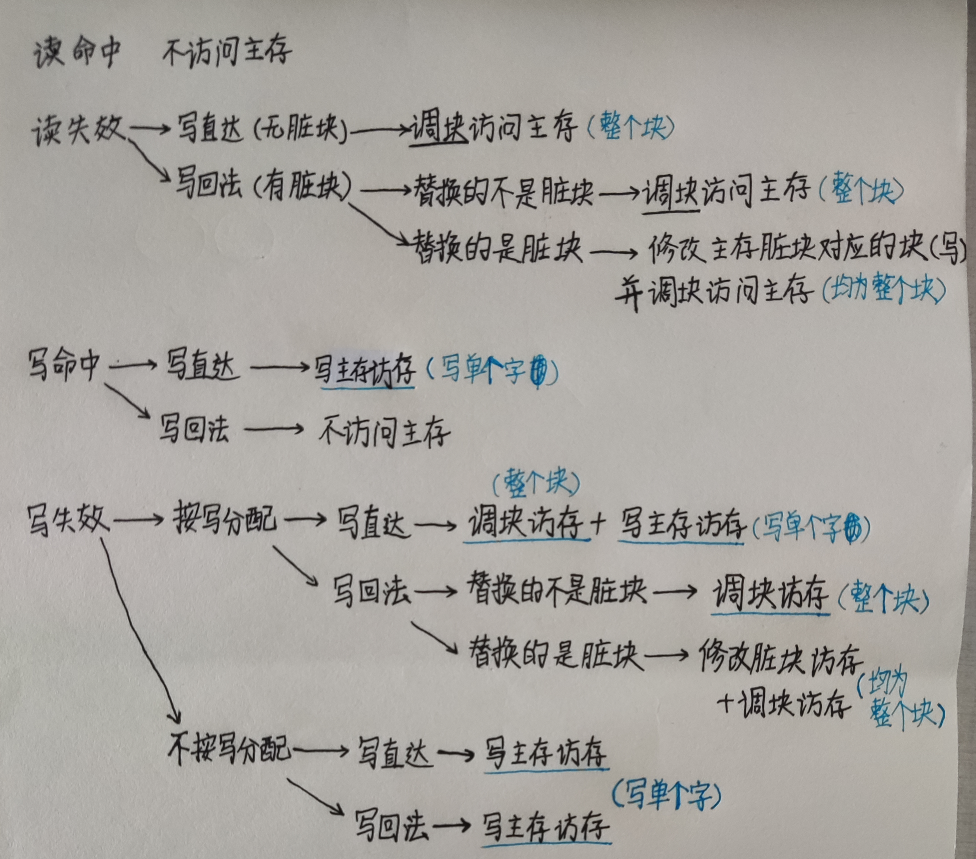
写策略
写直达和写回
写直达是两级都要写


写操作时的调块
按写分配在写不命中时需要将块调入cache再写入

Cache性能分析
==平均访存时间 = 命中时间+不命中率×不命中开销==
程序执行时间

例题:


Cache不命中对于一个CPI较小而时钟频率较高的CPU来说,影响是双重的(假设不命中代价(单位是时钟周期数)固定)

改进Cache性能
伪相联cache
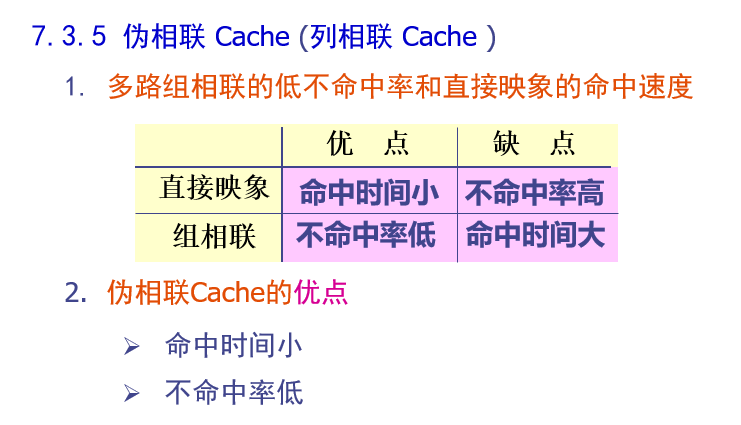
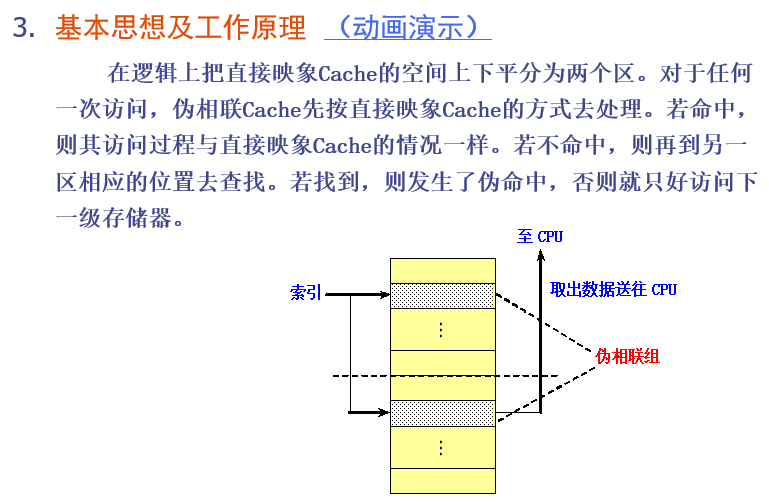
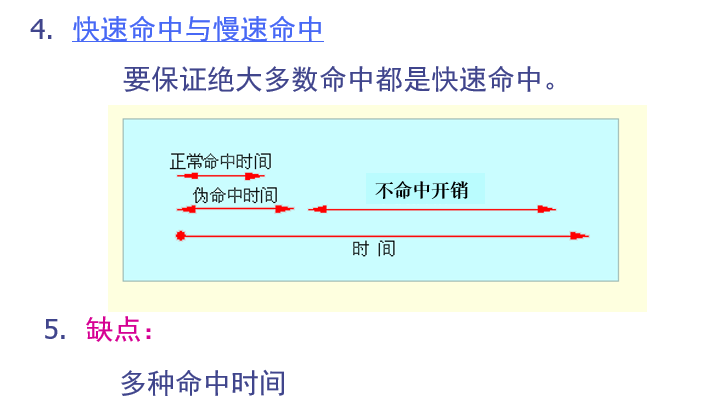
伪相联 Cache 具有一快一慢两种命中时间,它们分别对应于正常命中和伪命中的情况
减少cache不命中开销
两级cache
平均访存时间
全局不命中率和局部不命中率
每条指令的平均访存停顿时间



作业题
例7.3
平均访存时间
全局不命中率和局部不命中率
每条指令的平均访存停顿时间


求每次访存的平均停顿时间,还要用平均访存时间减去1,即平均访存时间减去第一级cache的命中时间
7.10
平均访存时间和CPU时间
平均访存时间=命中时间+失效率×失效开销
CPUtime=(CPU执行周期数+存储停顿周期数)×时钟周期
CPUtime=(IC×CPI执行周期数+总访存失效次数×失效开销)×时钟周期=IC×(CPI执行×时钟周期+每条指令的访存次数失效率失效开销×时钟周期)
平均访存时间不用×指令条数IC,而CPU时间需要×指令条数IC
选择时优先选择CPU时间更小的


7.11

2路组相连的一路命中就是直接命中,一路未命中二路命中就是伪命中,一路二路都未命中就是未命中

7.14
写回法:写的时候不需要访存,只往cache里写
写直达法:需要访存一次,cache和主存都要写
写不命中时的策略:
按写分配:写不命中时,先把所写单元所在的块调入Cache,
再行写入
不按写分配:写不命中时,直接写入下一级存储器而不调块
第八章 I/O系统
平均无故障时间MTTF(Mean Time To Failure)从开始投入工作,至产品失效的时间平均值
平均修复时间MTTR(Mean Time To Repair)设备处于故障状态时间的平均值
平均故障间隔时间MTBF(Mean Time Between Failures)两次故障间的时间平均值
$$
MTBF=MTTF+MTTR\
可用性=\frac{MTTF}{MTTF+MTTR}
$$
MTTF越长越好,MTTR越短越好
MTTF的倒数就是系统的失效率
如果系统中每个模块的生存期服从指数分布,则系统整体的失效率是各部件的失效率之和
I/O系统
反映外设可靠性能的参数有:
可靠性(Reliability)
可用性(Availability)
可信性(Dependability)系统的可靠性:系统从某个初始参考点开始一直连续提供服务的能力
用平均无故障时间MTTF(Mean Time To Failure)来衡量
系统中断服务的时间用平均修复时间MTTR(Mean Time To Repair)来衡量
产品的寿命特性:
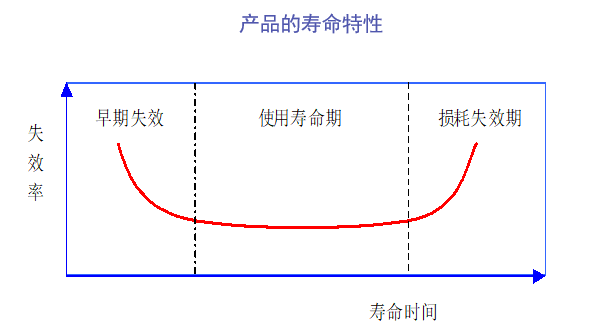
MTTF的倒数就是系统的失效率
系统的可用性:
平均故障间隔时间MTBF(Mean Time Between Failures)

系统的可信性:服务的质量。即在多大程度上可以合理地认为服务是可靠的。(不可以度量)
可靠性框图/串并联系统
串联模型计算示意

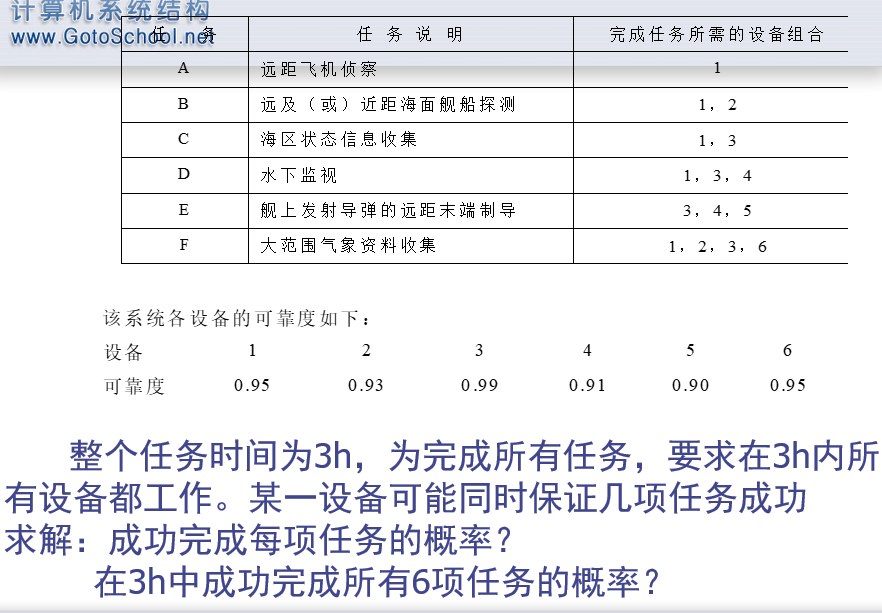
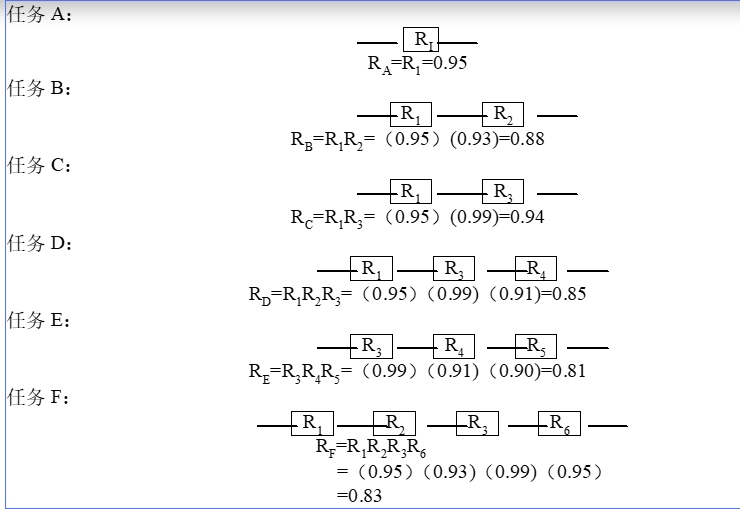
任务A~F都是串联,各自的计算都是直接可靠度相乘
下图注意红色部分:



MTTF的倒数就是系统的失效率
==如果系统中每个模块的生存期服从指数分布,则系统整体的失效率是各部件的失效率之和==
MTTF的叠加如同电阻的并联,越并越小
RAID


N个磁盘叠加,MTTF变为原来的1/N
题目
重要的:RAID0、1、4、5、6、10、01
考RAID,而且还要画框图,还要算可靠性,大概率考RAID0/1/01/10
框图中,RAID0就是串联,RAID1就是并联
提出进一步增强系统可靠性的若干建议:
四到八个控制器做多活,ECC
DRAM,RAID6,parity(spare) declustering
第九章 互连网络
互连网络是一种由开关元件按照一定的拓扑结构和控制方式构成的网络,用来实现计算机系统中结点之间的相互连接
互连函数
函数反映的是输入端与输出端 端号 的连接关系


基本互连函数
恒等函数I
交换函数E
立方体互连函数Cube
均匀洗牌函数$\sigma$
逆均匀洗牌函数$\sigma^{-1}$
蝶式函数$\beta$
反位序函数$\rho$
移数函数$\alpha$
PM2I函数
恒等函数

交换函数


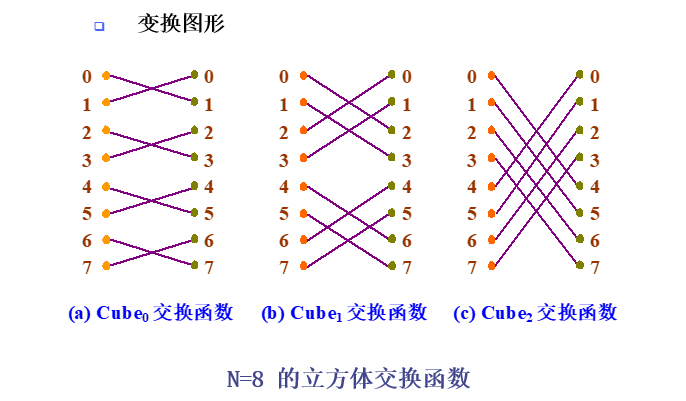
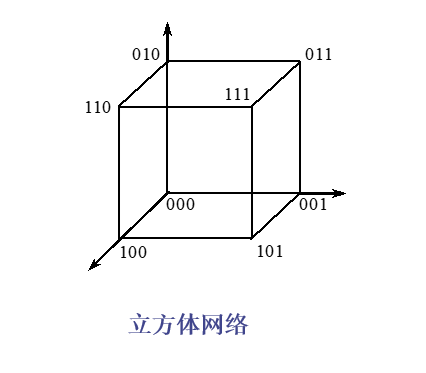
立方体网络:
均匀洗牌函数


子函数和超函数不是均分为两部分,而是取低k位和高k位
逆均匀洗牌函数:
将输入端的二进制编号循环右移一位而得到所连接的输出端编号
蝶式函数

反位序函数

移数函数
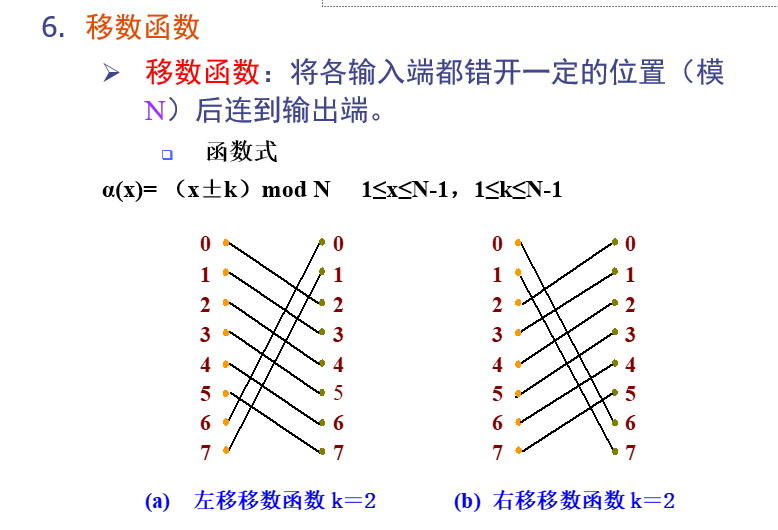
PM2I函数

阵列计算机ILLIAC Ⅳ
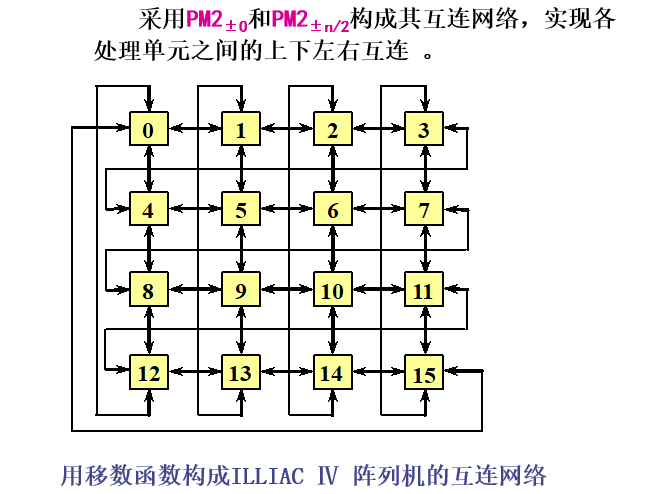
例9.1
记清楚所有的互连函数即可
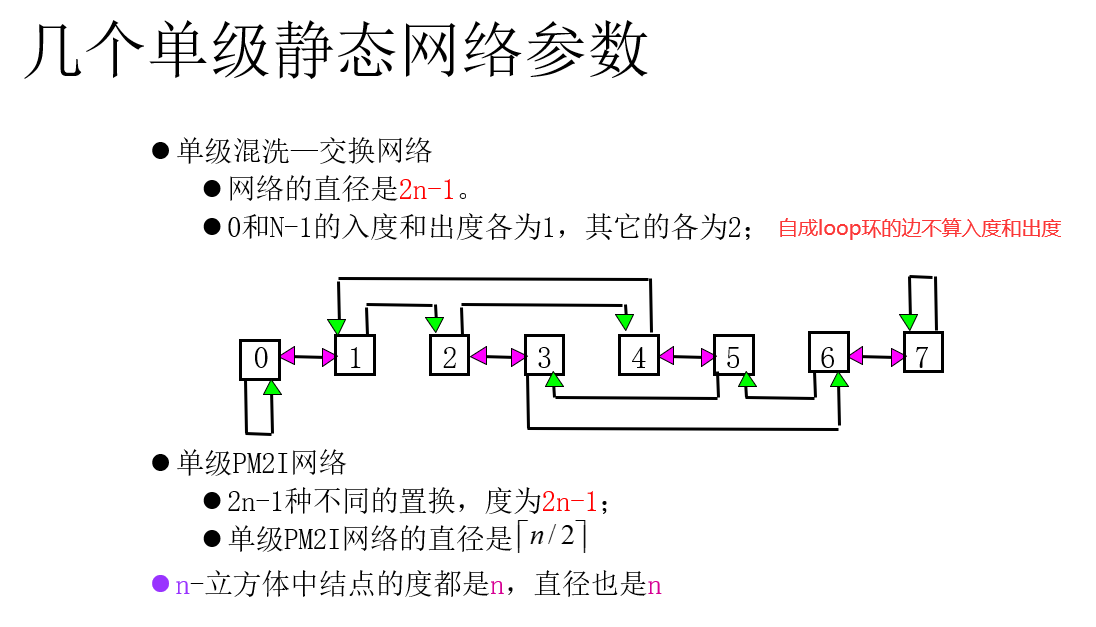
互连网络的结构参数和性能指标
主要参数
网络规模N:网络中结点的个数
结点度d:与结点相连接的边数(通道数),包括入度和出度
结点距离:对于网络中的任意两个结点,从一个结点出发到另一个结点终止所需要跨越的边数的最小值
网络直径D:网络中任意两个结点之间距离的最大值。
网络直径应当尽可能地小
等分宽度b:把由N个结点构成的网络切成结点数相同(N/2)的两半,在各种切法中,沿切口边数的最小值。
性能指标
静态互连网络
各结点之间有固定的连接通路、且在运行中不能改变的网络
所有类型的静态互连网络参数一览表
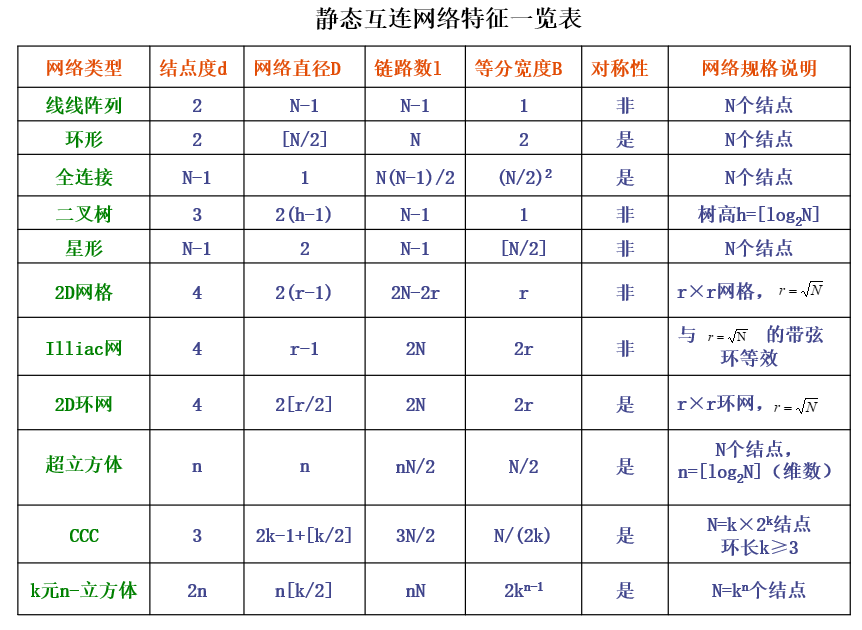
动态互连网络
多级互连网络
a×b开关:a个输入和b个输出

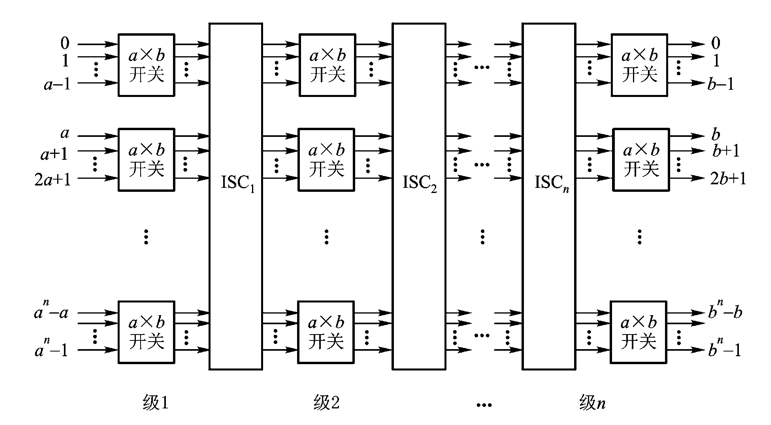
2×2开关
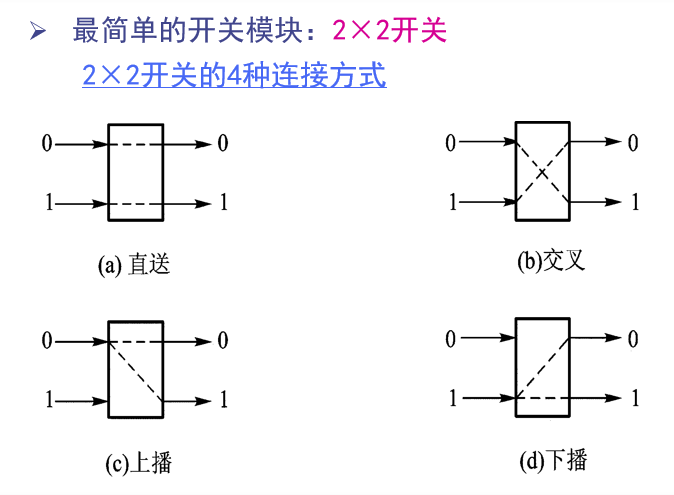
多级互连网络的区别:

Omega网络
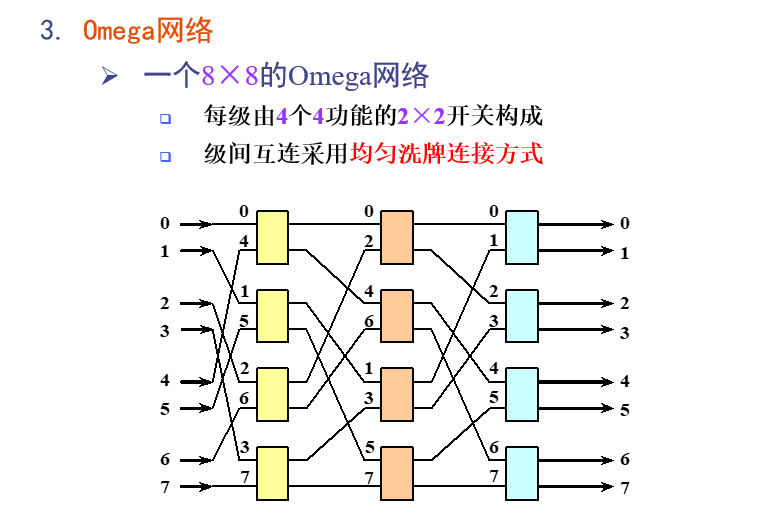
还考过16×16的
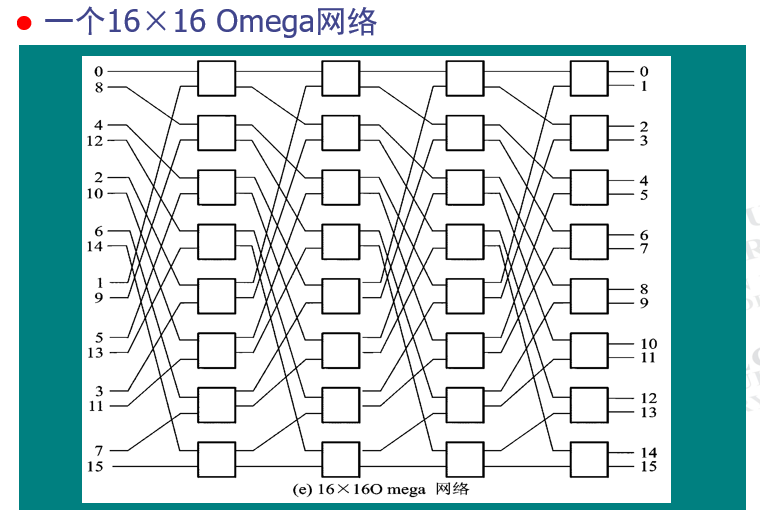
题目
恒等函数I
交换函数E
立方体互连函数Cube
均匀洗牌函数$\sigma$
逆均匀洗牌函数$\sigma^{-1}$
蝶式函数$\beta$
反位序函数$\rho$
移数函数$\alpha$
PM2I函数
9.9
(直径和节点度好像都不考)
混洗交换网络,就是混洗$\sigma$+交换$Cube_x$,两种方式同时起作用
混洗,等同于左移1位;交换,等同于某个特定的位取反
第一问一定要算对啊
处理器的个数是32个,所以高位要补0补到5位
求距离,就是看最少经过几步 移位/取反 ,能得到目标数字
循环移数网络
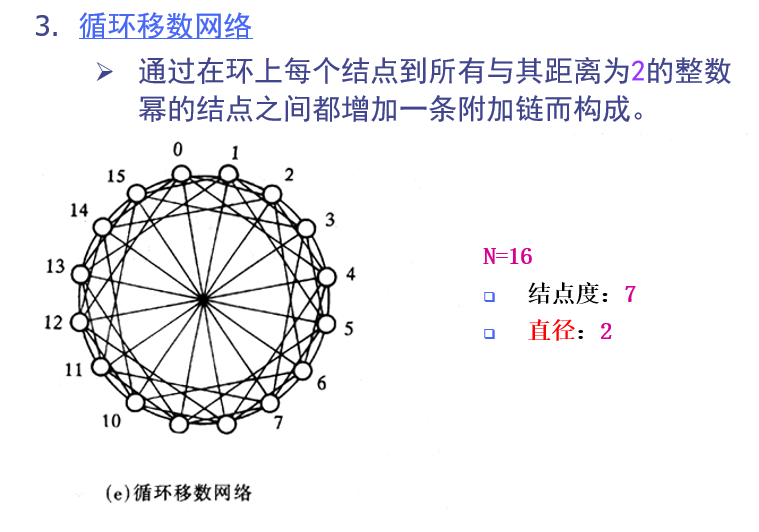


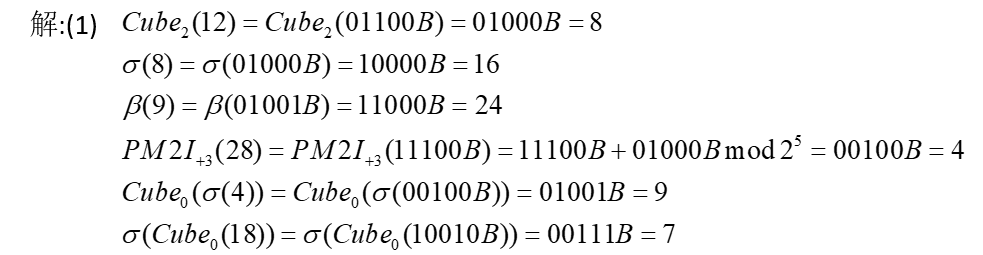

第三问用广度优先遍历,找到最远的处理机
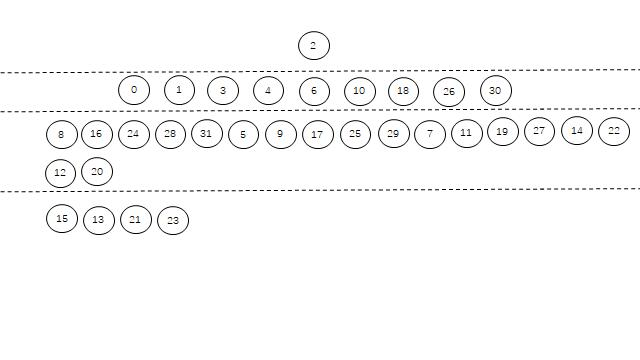
这个过程是对每层的每个数都要+1,-1,+2,-2,+4,-4,+8,-8,+16,-16取余,如果有新数,就写到下一层,否则跳过
9.13

整个图都要画
“走迷宫”
第十章 多处理机
应该就考这个
$1GHz=1\times 10^9Hz$


- 本文链接:https://wan-nan.github.io/2022/05/07/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%B3%BB%E7%BB%9F%E7%BB%93%E6%9E%84%E5%A4%8D%E4%B9%A0/
- 版权声明:本博客所有文章除特别声明外,均默认采用 许可协议。