662.二叉树最大宽度
每一层的 宽度 被定义为该层最左和最右的非空结点(即,两个端点)之间的长度。将这个二叉树视作与满二叉树结构相同,两端点间会出现一些延伸到这一层的 null 结点,这些 null 结点也计入长度。
契机是上面这道每日一题,要计算包含空结点在内的二叉树的最大宽度。
自己做的时候硬写了个层序遍历加很多标志位和判断,最后还是超时。
这道题最正确的解法应该是利用二叉树的顺序存储,只是除此之外还要注意数据范围,需要用unsigned long long这一最大的整型才不会溢出(实际上3k个结点还是有溢出的可能,只不过可以通过力扣的全部测试用例)
要结合二叉树的层序遍历,得到每一层的最小序号和最大序号
不过还是要套一层层序遍历的外皮,里面计算每个结点的下标,在每一层用最大的减去最小的再加一即为这一层的宽度
树的一些概念
结点的度:(和图论中的度定义不同)结点拥有的子树数目称为结点的度。
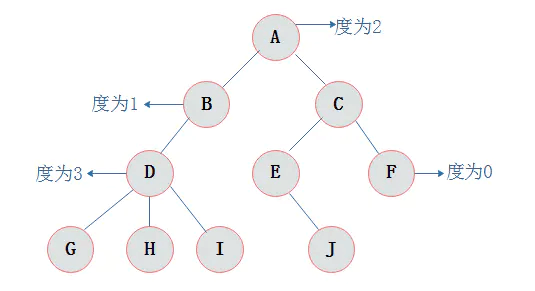
树的度:树中所有结点的度的最大值
树的类型
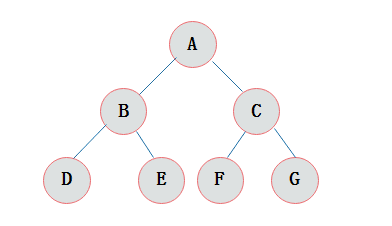
满二叉树
在一棵二叉树中。如果所有分支结点都存在左子树和右子树,并且所有叶子都在同一层上,这样的二叉树称为满二叉树。例如下面的树:
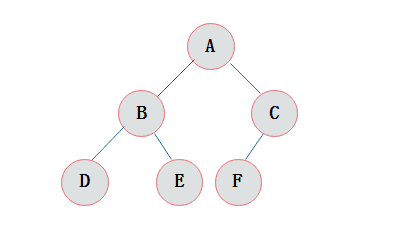
完全二叉树
若设二叉树的深度为k,除第 k 层外,其它各层 (1~k-1) 的结点数都达到最大个数,第 k 层所有的结点都连续集中在最左边,这就是完全二叉树。
平衡二叉树
是一棵空树或它的任意结点的左右两个子树的高度差的绝对值不超过1
完全二叉树一定是平衡二叉树
二叉查找树
对于树中的每个结点X,他的左子树中所有关键字值小于X的关键字值,而他的右子树中所有关键字值大于X的关键字值。
平衡二叉搜索树(AVL):是二叉搜索树和平衡二叉树的结合。
最优二叉树
树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree)。
哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近。
哈夫曼树也可以用于前缀编码。
可变长度编码比固定长度编码要好得多,其特点是对频率高的字符赋以短编码,而对频率较低的字符则赋以较长一些的编码,从而可以使字符的平均编码长度减短,起到压缩数据的效果。
哈夫曼编码是一种被广泛应用而且非常有效的数据压缩编码。若没有一个编码是另一个编码的前缀,则称这样的编码为前缀编码。
例子:
二叉堆
每个结点的值都大于其左孩子和右孩子结点的值,称之为大根堆;每个结点的值都小于其左孩子和右孩子结点的值,称之为小根堆。
堆不是平衡二叉搜索树,搜索树是中大于左小于右,堆是父结点值大于(小于)左右孩子结点值
==红黑树==
B树和B+树【一定常看】
什么是BST?
什么是AVL树?
什么是B树?
什么是B+树?
各自的好处和缺点?
上面的链接从BST(Binary Search Tree二叉搜索树)到AVL(Adelson-Velsky and Landis Tree平衡二叉搜索树)到B树再到B+树
按顺序引入,好文章
一棵4阶B+树
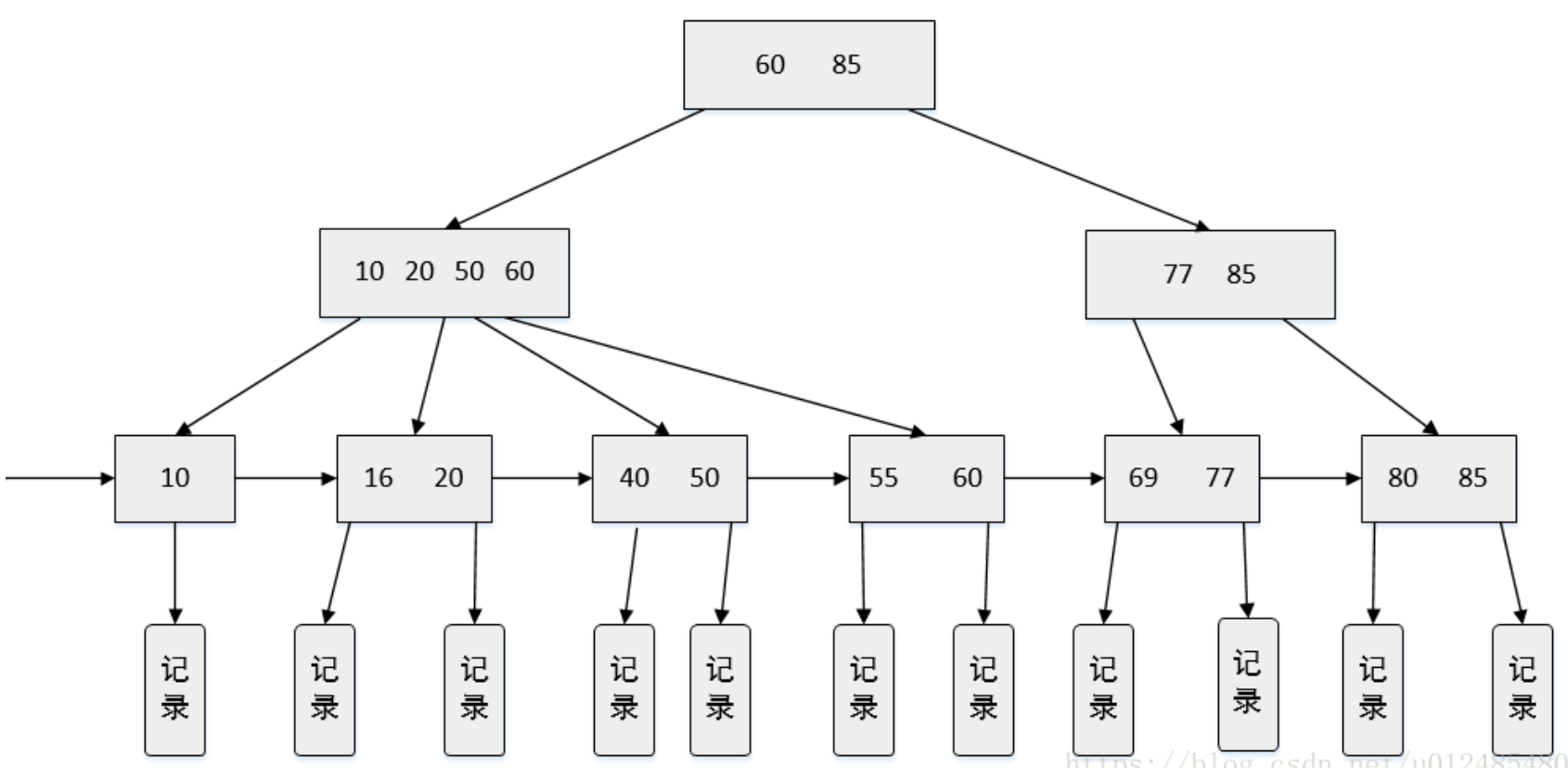
B+树和B树最大的不同是:
- B+树内部有两种结点,一种是索引结点,一种是叶子结点。
- B+树的索引结点并不会保存记录,只用于索引,所有的数据都保存在B+树的叶子结点中。而B树则是所有结点都会保存数据。
- B+树的叶子结点都会被连成一条链表。叶子本身按索引值的大小从小到大进行排序。即这条链表是 从小到大的。多了条链表方便范围查找数据。
- B树的所有索引值是不会重复的,而B+树 非叶子结点的索引值 最终一定会全部出现在 叶子结点中。
B树的好处和不足:
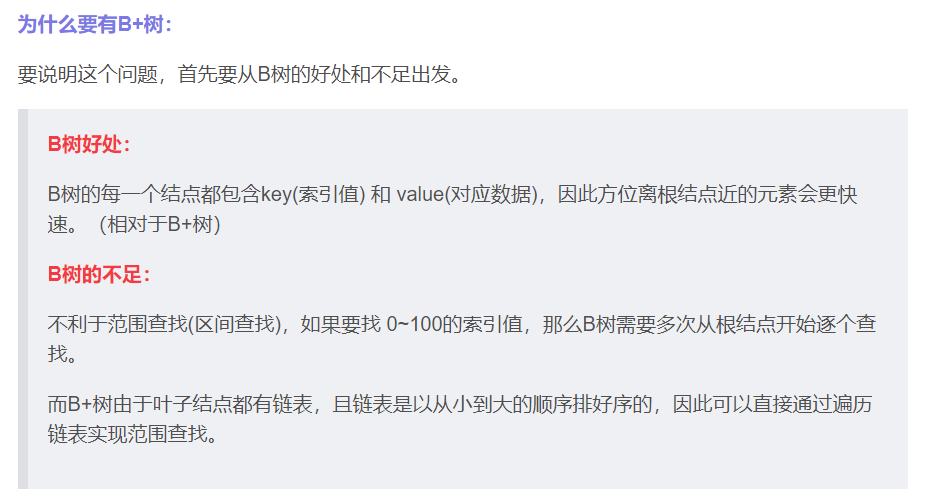
线索二叉树【一定常看】
线索二叉树的结构:
什么是线索二叉树?
对于n个结点的二叉树,在二叉链存储结构中有n+1个空链域,利用这些空链域存放在某种遍历次序下该结点的前驱结点和后继结点的指针,这些指针称为线索,加上线索的二叉树称为线索二叉树。
知道了“前驱”和“后继”信息,就可以把二叉树看作一个链表结构,从而可以像遍历链表那样来遍历二叉树,进而提高效率。
二叉树的存储
对于完全二叉树,可以基于数组采用顺序存储结构
顺序存储简单来说,就是下标为
i的结点,左孩子储存在下标为2*i的位置,右孩子储存在下标为2*i+1的位置这也正是最上面那道题目的解法,利用顺序存储标记出每一层的起始结点和末尾结点的下标,作差加一即可得到答案
除此之外,顺序存储还有双亲表示法:
对于非完全二叉树,则基于链表采用链式存储结构
例如二叉链表、三叉链表等
链式存储主要是两种:孩子表示法和孩子兄弟表示法
孩子表示法类似图的存储,使用邻接链表
孩子兄弟表示法即为我们常用方法
这种方法弊端是找双亲比较麻烦,可以通过为每个结点增设一个parent域指向父结点来解决
二叉树的遍历
精简的总结:X序遍历→父结点在遍历顺序中的位置(一定是先遍历左子树,再遍历右子树)
前序遍历:父结点->左子树->右子树
中序遍历:左子树->父结点->右子树
后序遍历:左子树->右子树->父结点
以上三种遍历都是基于栈(递归)
层序遍历基于队列,详见1302.层数最深叶子节点的和(层序遍历)
遍历可能的考察方式:
【错!!】给定一棵二叉树的前序遍历/中序遍历后序遍历三种序列中的两种,要求确定出这棵二叉树
注意:已知前序遍历序列和后序遍历序列,不可以唯一确定一棵二叉树。
可以的组合:
- 前序+中序
- 中序+后序
- 中序+层序