数据结构-图-总结

继之前的二叉树总结之后，由于图也是数据结构中一个重要的部分，还涉及一些离散的知识，所以也单独成文进行总结。

C++中的构造函数

struct node{
	node(int c)
	{
		x=c;
		y=z=0;
	}
	int x,y,z;
};

图的一些概念

无向图：顶点间的边为无序对

有向图：顶点间的边为有序对
简单图：不存在重复边和自环的图

多重图：与简单图相对
完全图：具有n个顶点和n(n-1)/2条边的无向图

有向完全图：具有n个顶点和n(n-1)条边的有向图，每两个顶点之间都有两条方向相反的边连接的图。
连通：在无向图中，若从顶点v到顶点w有路径存在，则称v和w是连通的。

连通图：图中任意两个顶点都是连通的

连通分量：无向图的极大连通子图称为连通分量
强连通图：有向图中，任意两个顶点之间都有双向路径

强连通分量：有向图中的极大强连通子图

一般对于有向图讨论的是其强连通性

而无向图只讨论其连通性
生成树：连通图的生成树是包含图中全部顶点的一个极小连通子图。若图中顶点数为n, 则它的生成树含有n − 1条边。

注意:包含无向图中全部顶点的极小连通子图，只有生成树满足条件，因为砍去生成树的任一条边，图将不再连通。
顶点的度、入度和出度
网：图中的边可以带权，带权图称为网
若一个图有n个顶点，并且有大于n − 1条边，则此图一定有环

图的存储结构

邻接矩阵

提前开好$n\times n$的二维数组（形似矩阵）

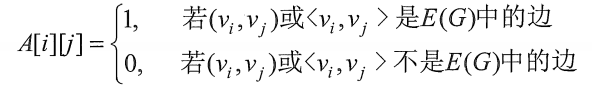
无向图的邻接矩阵一定是对称矩阵
邻接表

对于稀疏图，边数较少，邻接矩阵会耗费大量的空间，此时使用邻接表

也有逆邻接表来方便入度的计算
十字链表：
十字链表是有向图的一种链式存储结构。

十字链表的好处就是因为把邻接表和逆邻接表整合在了一起，这样既容易找到以V为尾的弧，也容易找到以V为头的弧，因而容易求得顶点的出度和入度。

而且它除了结构复杂一点外，其实创建图算法的时间复杂度是和邻接表相同的，因此，在有向图的应用中，十字链表是非常好的数据结构模型。
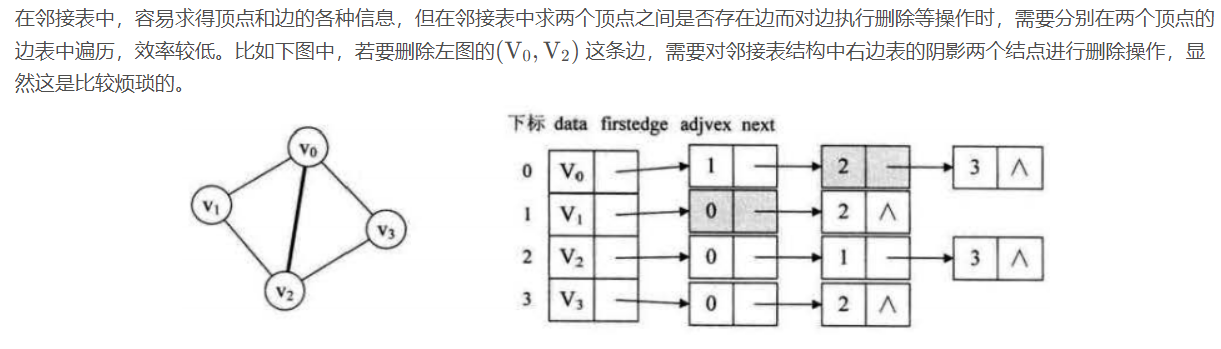
邻接多重表：

邻接多重表是无向图的另一种链式存储结构。
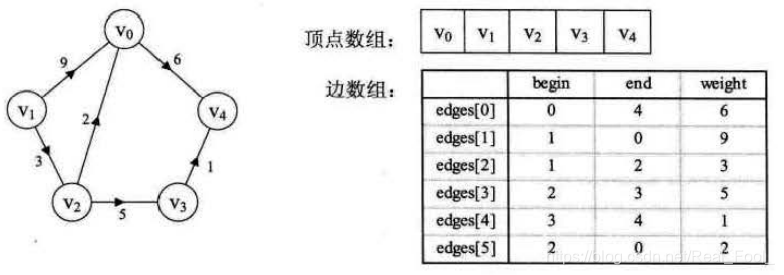
边集数组

更适合对边依次进行处理的操作，而不适合对顶点相关的操作。

图的重要算法

最小生成树（Prim&Kruskal）

最小生成树（Minimum Spanning Tree）：图的所有生成树中具有边上的权值之和最小的树。

两种算法的实现比上面链接里友好的代码

基于带权图得到最小生成树的方法：

普里姆（Prim）算法：从任意一个结点出发进行繁衍

时间复杂度$O(n^2)$，适合稠密图

unordered_set<Edge, EdgeHash, EdgeEqual> primMST(Graph graph){
    // 装边的最小堆
    auto cmp = [](const Edge& e1, const Edge& e2){
        return e1.weight > e2.weight;
    };
    priority_queue<Edge, vector<Edge>, decltype(cmp)> smallQueue(cmp);
    // 判断节点是否访问过
    unordered_set<Node, NodeHash, NodeEqual> node_set;
    unordered_set<Edge, EdgeHash, EdgeEqual> result;
    for(auto ite: graph.nodes){
        if(node_set.find(*ite.second) == node_set.end()){
            // 如果没有访问,将其标记为访问过，并把它对应的边放入最小堆
            node_set.insert(*ite.second);
            for(Edge* edge: ite.second->edges){
                smallQueue.push(*edge);
            }
            // 在当前这个图中寻找最小生成树
            while(!smallQueue.empty()){
                // 从堆中取出一个最小权重边，并取出对应节点
                Edge help_edge = smallQueue.top();
                smallQueue.pop();

                Node edge_to = *(help_edge.to);
                // 然后判断这个节点是否被访问过，如果没有则将这个边加入边集
                if(node_set.find(edge_to) == node_set.end()){
                    result.insert(help_edge);
                    node_set.insert(edge_to);   // 标记edge_to也已经访问过了
                    for(Edge *newEdge: edge_to.edges){
                        smallQueue.push(*newEdge);
                    }
                }
            }
        }
    }
    return result;
}

克鲁斯卡尔（Kruskal）算法【贪心】：按照权值从小到大的顺序依次选取图中的边，同时确保不会成环（并查集）

时间复杂度$O(eloge)$，适合稀疏图

unordered_set<Edge, EdgeHash, EdgeEqual> kruskalMST(Graph graph){
    auto cmp = [](const Edge& a, const Edge& b){
        return a.weight > b.weight;    // 最小堆
    };
    vector<Node*> list;
    for(auto ite: graph.nodes){
        list.push_back(ite.second);
    }
    UnionFindSet unionFind(list);   // 建立并查集
    priority_queue<Edge, vector<Edge>, decltype(cmp)> smallQueue(cmp);
    for(auto edge: graph.edges){
        smallQueue.push(*edge);
    }
    // 构造选中的输出边集
    unordered_set<Edge, EdgeHash, EdgeEqual> result;
    while(!smallQueue.empty()){
        Edge edge = smallQueue.top();

        smallQueue.pop();
        if(!unionFind.isSameSet(edge.from, edge.to)){  
// 判断是否为一个环，如果一个边的两端节点为一个集合，那么必为一个闭合环
            result.insert(edge);
            unionFind.Union(edge.from, edge.to);
        }
    }
    return result;
}

稠密图是边的数量较多。稠密和稀疏是对于边的数量来说的

Kruskal算法时间复杂度和边数e相关，所以适合稀疏图，使用邻接表存储

Prim算法时间复杂度只和结点数n相关，所以适合稠密图，使用邻接矩阵存储

最短路径

无权图：单源最短路径问题使用BFS解决【同时要求边没有权重】
对于带权图
- 单源最短路径用迪杰斯特拉
  
  本质是动态规划，时间复杂度$O(V^2)$
  
  画一个表辅助解题
- 多源最短路径用弗洛伊德
  
  本质是动态规划，时间复杂度$O(V^3)$（因为把任意两个点之间的最短距离都算出来了）
  
  画多个表辅助解题