LEETCODE

打勾的是当时自己动手做出来的

加粗的是当时有问题的

来源：🔥 LeetCode 热题 HOT 100 & 每日一题 & 以前做过的题目 & 周赛题目

周赛题目总结：【灵茶山艾府】2022 年周赛题目总结（上篇） 从周赛中学算法 - 2022 年周赛题目总结（下篇）

做题的时候尽量带着纸笔在纸上比比划划

• 注意点：

  • 结果对1e9+7取模：

    注意可能出现的负数，要先判断是负数，才能先加再模，不然可能出现取模之前就会因为加了1e9+7而整数溢出

    if(dp[i][j]<0)
        dp[i][j]+=1000000007;
    dp[i][j]%=1000000007;

  • 【整数溢出】long long用long代替（因为现在都是64bits的机器，所以可以这么写）

• 很容易见到的方法

  • 二分

    最简单的二分要求单调，但是也可以值域二分（最小化最大值）

    6346、6355、4、34

    很难逐步确定答案，但是可以确定答案的上下界，同时验证答案是否正确的复杂度很低

    int l=lower_bound(nums.begin(),nums.end(),lower)-nums.begin();
    int r=upper_bound(nums.begin(),nums.end(),upper)-nums.begin();

  • 动态规划

    1130（区间dp）、53/1186（最大子数组和）、1911、834、2681（结合数学）

  • 双指针（滑动窗口）

    1234、75、3、1616

  • 预处理

    6340、42

    • 前缀后缀

      6357

    • 前缀和+哈希

      1124、560、1590、面试题 17.05、2488

  • 单调栈

    456、239（模拟单调队列）、42、

    （常常辅之以预处理）

  • 二叉树（回溯、递归）

    1145、1373、1080、979

  • 贪心

    1145

  • STL使用

  • Trie树

    208、648

  • 字符串处理

  • 图论

    • 欧拉回路

    • 拓扑排序（保存入度和全图）

      210

    • DFS/BFS

      n1、1210、1079、1091

      好久没遇到，以至于这种简单暴力的方法反而很陌生

      BFS比DFS陌生

• 【时间复杂度控制】

  一般ACM或者笔试题，或者力扣上的题目的时间限制是1秒或2秒。

  在这种情况下，C++代码中的操作次数控制在 1e7 为最佳。

  ---

  1. $$n≤30$$

     指数级别，dfs+剪枝，状态压缩dp

  2. $$n≤100 → O(n^3)$$

     floyd，dp，高斯消元

  3. $$n≤10^3 → O(n^2)，O(n^2logn)$$

     dp，二分，朴素版Dijkstra、朴素版Prim、Bellman-Ford

     分界点（一旦n到达$$10^4$$，就不适合n^2^的暴力解法）

  4. $$n≤10^4 → O(n\sqrt{n})$$

     块状链表、分块、莫队

  5. $$n≤10^5 → O(nlogn)$$

     各种sort，线段树、树状数组、set/map、heap、拓扑排序、dijkstra+heap、prim+heap、Kruskal、spfa、求凸包、求半平面交、二分、CDQ分治、整体二分、后缀数组、树链剖分、动态树

  6. $$n≤10^6 → O(n), 以及常数较小的 O(nlogn) 算法$$

     单调队列、 hash、双指针扫描、并查集，kmp、AC自动机

     常数比较小的 O(nlogn) 的做法：sort、树状数组、heap、dijkstra、spfa

  7. $$n≤10^7 → O(n)$$

     双指针扫描、kmp、AC自动机、线性筛素数

  8. $$n≤10^9 → O(√n)$$，

     断质数

  9. $$n≤10^{18} → O(logn)$$

     最大公约数，快速幂，数位DP

---

• 78.子集

  • mask
  • DFS

• 297. 二叉树的序列化与反序列化

  • 前中后序遍历
  • 层序遍历

  参考题解

  后面重温的过程中发现：【超出内存限制】指的是爆栈

  因为将字符串中间结果作为参数在传递，这个过程比较占空间

  后续改成只保存一个全局变量即可通过

  （所以全局变量相较于堆栈传参也是有好处的）

• 55. 跳跃游戏

• **23. 合并K个升序链表**【好题】

  1e6的数据不能犯蠢用排序

  O(n)时间+O(1)空间 合并链表

  合并两个有序链表：

  ListNode* mergeTwoLists(ListNode *a, ListNode *b) {
      if ((!a) || (!b)) return a ? a : b;
      ListNode head, *tail = &head, *aPtr = a, *bPtr = b;
      while (aPtr && bPtr) {
          if (aPtr->val < bPtr->val) {
              tail->next = aPtr; aPtr = aPtr->next;
          } else {
              tail->next = bPtr; bPtr = bPtr->next;
          }
          tail = tail->next;
      }
      tail->next = (aPtr ? aPtr : bPtr);
      return head.next;
  }

  • （暴力）多次重复双指针【会暴力的即可】
  • （分治）联想归并排序的merge环节
  • （堆排序）联想堆排序

  参考题解

  共n个子链表，每个子链表最长有k个元素，当k=1时不就是正常的排序吗？

  上面的三种解法其实也就对应三种排序算法

• 238. 除自身以外数组的乘积

  序列乘积与序列之和的区别是可以减，但是除法会遇到0出问题

• 152. 乘积最大子数组

  （动态规划），还与和最大的子数组的转移方程不同

  用 $f_{\max}(i)$ 来表示以第 i 个元素结尾的乘积最大子数组的乘积

  用 $f_{\min}(i)$ 来表示以第 i 个元素结尾的乘积最小子数组的乘积

• 5. 最长回文子串

  （动态规划）找到可以用于转移方程的性质，本题中是回文串两边各去掉一个字符仍然是回文串

  按照length从小到大进行规划即可

  （中心扩展算法）枚举所有可能的回文串中心，向两边扩张，找到最长的

  这道题只要不是暴力，$O(n^2)$就能过

  要先从暴力解法出发，想办法优化，暴力遍历所有可能的子串复杂度$O(n^2)$，判断每个子串是否是回文串复杂度$O(n)$，后者这个过程可以优化，使用dp复用之前的结果

• 338. 比特位计数

  入门（动态规划）

• 560. 和为 K 的子数组

  还是那个思路：先写暴力，再优化

  本来想法是双指针，后面看到数据可能是负的，没有单调性，所以不能用双指针

  前缀和+哈希

  （和1124很像）

• 101. 对称二叉树

  迭代的方法不好想，进入队列的顺序比较关键

• 200. 岛屿数量

  用bfs，更改标记数组的时机居然导致了被卡时间，我不理解

• 538. 把二叉搜索树转换为累加树

  中序遍历的变体

• 448. 找到所有数组中消失的数字

• 102. 二叉树的层序遍历

• 15. 三数之和

  数组中三个数之和为0的所有组合

  还是那个思路：先想到$O(n^3)$的暴力，再用哈希去优化

  还有就是如何避免出现重复的三元组：先排序，再避免i/j处的值与前一个i/j相同

  • 还可以变体为：三个数之和为任意一个给定常数

    思路都是先排序，然后用左右双指针或用unordered_map存储最右边的位置，复杂度都是$O(n^2)$

  • 但是这道题：16. 最接近的三数之和只能用双指针

    要是上面这题怎么优化，则是用各种判断提前退出循环的方式优化，参考

• 84. 柱状图中最大的矩形

  单调栈的应用：一遍遍历求所有元素两边第一个比其小的元素的位置

  一个元素进入单调递增栈后，左侧相邻的元素是左侧第一个比它小的元素；

  元素被pop()出栈时，为了进栈将其挤出去的元素是右侧第一个比它小的元素；

  ---

  本来只能写个$O(n^2)$的暴力，但是看了题目的tag有单调栈，就往这里想，最后写出来的，没看题解但看了tag

  一道hard交了六次，后面头都是晕的了

  

• 206.反转链表

• 19. 删除链表的倒数第 N 个结点

  快慢指针（双指针）

• 17. 电话号码的字母组合

  简简单单dfs

• 2022/11/5暂时暂停吧

  啥都不会，找个🔨实习

  2022/12/20接着刷

• 1760. 袋子里最少数目的球

  二分变体（太久没做题，看了tag才想出来）

• 1759. 统计同构子字符串的数目

  1. 有求和就小心溢出，用long long int表示

  2. 只需返回对 1e9 + 7 取余 后的结果

     注意看题目的限制

     另外，如果可能会出现负数，最好用ans先加上1e9 + 7再取模

• 11. 盛最多水的容器

  双指针！！！！！

  不是单调栈，不要误会

  ==和84. 柱状图中最大的矩形对比，非常相似，但是一个是双指针，一个是单调栈==

• 449. 序列化和反序列化二叉搜索树

  递归，之前做过这题

• 70. 爬楼梯

  动态规划

• 124. 二叉树中的最大路径和

  遇到二叉树相关，八成要用递归，把每个子树都当成新的新的树看待

• nowcoder.36进制加法

  string.append(int cnt, char c)，在string的末尾添加cnt个字符c

• 855. 考场就座

  • STL的使用

    • set

      set.find()的返回值是iterator，前一个元素是prev(iterator)，后一个元素是next(iterator)

      集合的开始元素的iterator是set.begin()，结束元素是set.end()（正向迭代器）或set.rbegin()（反向迭代器）

      删除set中的元素：set.erase(value)

      if (p != *seats.begin() && p != *seats.rbegin()) {
          auto it = seats.find(p);
          pq.push({*prev(it), *next(it)});
      }

    • priority_queue：

      自定义类型的优先队列，重载<运算符，注意所有的关系运算符都是左结合的，所以bool operator<(const section& b) const{}的函数体要表达的应该是*this < b

      另外，按照上面的语义正确重载小于运算符，priority_queue是大顶堆，即优先级高的在堆顶；sort是从小到大排序

  • 延迟删除的思想

    priority_queue中只能出队top()，没办法立即删除中间位置的成员，所以可以做好标记，等用到的时候检查标记，有删除标记则进行删除

• 1801. 积压订单中的订单总数

  • 自定义类型的priority_queue以及<符号的重载

  • 只需返回对 1e9 + 7 取余 后的结果

    注意看题目的限制

    另外，如果可能会出现负数，最好用ans先加上1e9 + 7再取模

• 1802. 有界数组中指定下标处的最大值

  • 二分：【已知解的左右边界，求最优解】，$$check()的复杂度×logn$$
  • 有【大的数求和or单增数列求和】就小心溢出，用long long int表示

• 300. 最长递增子序列

  两种做法

  • $$O(n^2)$$ 动态规划
  • $$O(nlogn)$$ dp+贪心+二分

• 745. 前缀和后缀搜索

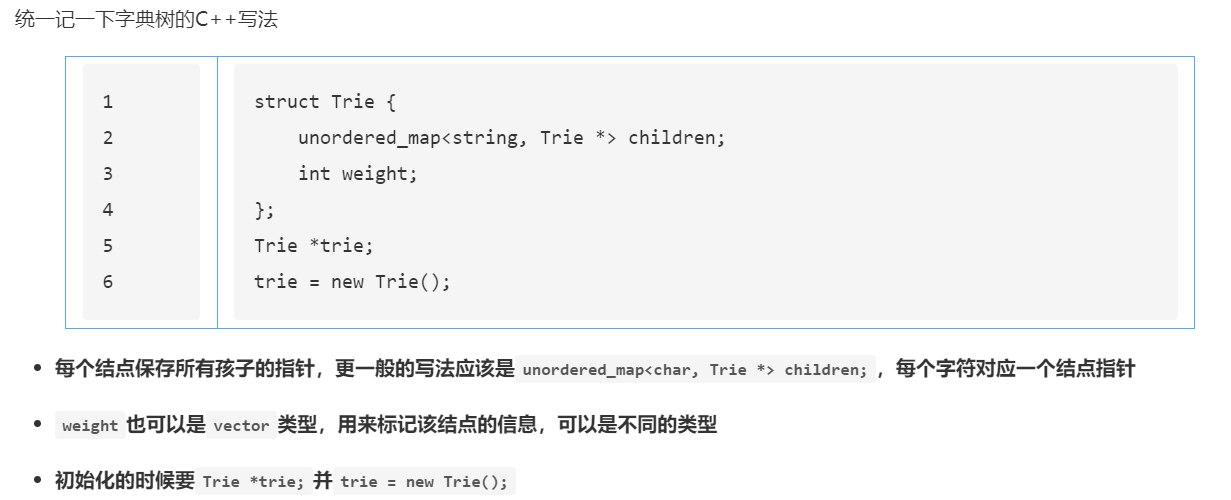
  22年暑假做的题目，当时的记录：745.前缀和后缀搜索（Trie写法）

  三种方法：单字典树/哈希/双字典树

  字典树的便捷写法可以记一下：

  

• 421. 数组中两个数的最大异或值

  经典的区间元素异或的问题，还是用字典树解决

  （还没上手做）

• 1803. 统计异或值在范围内的数对有多少

  （不仅没上手做，连怎么做还没看懂）

• 1658. 将 x 减到 0 的最小操作数

  正统做法应该是双指针（也可以叫做滑动窗口）

  我用的哈希做的，题目不难，但是可能方法比较陌生

• 总是容易漏掉很多情况

  下面这种写法不对，因为else if是和if(cond2)对齐的！！！

  if(cond1)
      if(cond2)
          return 0;
  else if(cond3)
      return 1;

• 2185. 统计包含给定前缀的字符串

  string.find(pref,0) == 0

  string.find()（参考）返回的是int（position），不是iterator

• 6284. 使字符串总不同字符的数目相等

  327th场周赛第三题，我直接怒写接近100行代码，实际上20行就能搞定，总是容易把题目想复杂

  可以再做一下，简单的模拟，但是容易写的很复杂

• 753. 破解保险箱

  欧拉回路

  可以把题目转化成在每个节点的入度和出度都为k的有向图中，找到一条欧拉回路，可以用DFS找欧拉回路

  参考

  （注意回路和通路不一样）

• 332. 重新安排行程

  和上面的题类似，但这个找的是欧拉通路，不过也是用DFS的方法找

  • 欧拉是每条边都只能走一次（如这个使用机票的行程问题）
  • 哈密顿是每个点都只能走一次（暂时还没遇到这类问题）

  priority_queue<int, vector<int>, greater<int> > pq;

  对priority_queue使用greater或less的方法如上，要注意priority_queue的less是大顶堆，greater是小顶堆，所以一般都用的是greater

• 1819. 序列中不同最大公约数的数目

  枚举每个可能的数字x，检验x是否是某个子序列的最大公约数

  • 怎么检验？

    要想x是序列An的最大公约数，则An中所有能够整除x的数 的 最大公约数 一定是 x

    如An中只有2x,4x，则不成立，子序列的最大公约数只能是2x

    但An中有2x,4x,5x，则成立

    即枚举x后，找出An中的所有可以整除x的数，求他们的gcd是否为x

    求多个数的gcd，可以将g初始化为0，再依次$$g=gcd(g,a_i)$$

• 1813. 句子相似性 III

  • 字符串处理典型题目

  • 双指针新奇题目

  这篇题解中的字符串分词写法可以记一下

• 1817. 查找用户活跃分钟数

  • 对于自定义类型，重载关系运算符就是在其类型声明中写一个operator重载函数

  • 但是对于已有类型，如vector，可以写一个cmp()函数，再sort(logs.begin(),logs.end(),cmp);这样调用即可

    static bool cmp(vector<int> &a, vector<int> &b){
        if(a[0]==b[0])
            return a[1]<b[1];
        return a[0]<b[0];
    }

    注意写在类中时要加static声明，表明其是类的静态函数成员，这样的函数没有this指针（一般的函数成员非静态，会有this指针，无法传入sort作为排序函数）

    不加static的报错及解决

    或者将自定义比较函数cmp()写在类外面，也没有this指针

    参考：恼人的函数指针：指向类成员的指针

• 1663. 具有给定数值的最小字符串

  在string前面添加字符，时间效率：

  string.append(int count, char c) + reverse

  >

  string = char(c) + string

  string.insert(int position, int count, char c)

  使用+运算符来拼接字符串比较耗时

• 6338. 猴子碰撞的方法数

  • C++快速幂求模

    $$a^b$$

    降低a的规模：a = a % mode

    降低b的规模：（若b为偶数）$$a^b=(a^2)^{\frac{b}{2}}$$；（若b为奇数）$$a^b=(a^2)^{\frac{b-1}{2}}\times a$$；再降低a的规模即可

    long long Mode(long long a, long long b, long long mode)
    {
        long long sum = 1;
        a = a % mode;
     
        while (b > 0) {
            if (b % 2 == 1)		//判断是否是奇数，是奇数的话将多出来的数事先乘如sum
                sum = (sum * a) % mode;
            b /= 2;
            a = (a * a) % mode;// 不断的两两合并再取模，减小a和b的规模
        }
        return sum;
    }

  • Python等直接用库函数

    class Solution:
        def monkeyMove(self, n: int) -> int:
            MOD = 10 ** 9 + 7
            return (pow(2, n, MOD) - 2) % MOD

• 1324模式和132模式

  • 456. 132 模式

    单调栈+预处理

    C++中multiset容器是STL模板库中一个非常有用的类型，它可以看成一个序列，插入一个数，删除一个数都能够在O(logn)的时间内完成，而且他能时刻保证序列中的数是有序的，而且序列中可以存在重复的数（而set容器要求两两不同，且不保证有序）。

  • 6340. 统计上升四元组

    视频题解

    维护二维前后缀预处理的值

    四元组：(i, j, k, l)满足0 <= i < j < k < l < n 且nums[i] < nums[k] < nums[j] < nums[l]

    $$O(n^2)$$遍历i和l，j和k通过二维前后缀预处理维护

    • 还有种做法是借助132模式的结果，题解（非常巧妙）

      但是132模式的数据量是2e5,1324模式的数据量是4k，所以后者可以用n^2^的算法，前者只能nlogn或者n

• n1. 寻友之旅

  BFS求最短路径

  很久没遇到忘记了

  • Golang的循环输入

    var a, b int
    for {
        _, err := fmt.Scan(&a, &b)
        if err == io.EOF {
            break
        }
        fmt.Println(a + b)
    }

• 42. 接雨水

  前后缀预处理参考题解 / 单调栈

• 1145. 二叉树着色游戏

  二叉树的DFS+贪心

  需要一点自己的思考

• **6346. 打家劫舍 IV**【周赛失利题目】

  二分+贪心（check函数需要借助贪心来check）

  虽然上来觉得不单调不能二分，但是这是另一种贪心的题型，最小化最大值，属于值域二分（另一种感觉可以叫定义域二分）

• 1210. 穿过迷宫的最少移动次数

  BFS求最短路径

  不同之处是需要多一个维度来表示蛇的方向，其他都大同小异

• 1797. 设计一个验证系统

  一边遍历map一边删除其中的元素

  问题：

  1. 要使用迭代器完成这件事，不能使用auto
  2. mp.erase(it);之后it会失效，而mp.erase(it)会返回next(it, 1)，所以要使用it来接住其返回值

  所以需要像下面这样写，删除的时候不需要it++，没删除的时候需要it++

  for (auto it = mp.begin(); it != mp.end();)
  {
      if (it->second <= currentTime)
      {
          it = mp.erase(it);
          continue;
      }
      it++;
  }

• 1223. 掷骰子模拟

  dp题，递推方程刚开始想错了写了很久（高中排列组合没学好）

  • 如果出现结果需要对1e9+7取模：

    注意可能出现的负数，要先判断是负数，才能先加再模，不然可能出现取模之前就会因为加了1e9+7而整数溢出

       if(dp[i][j]<0)
           dp[i][j]+=1000000007;
    dp[i][j]%=1000000007;

    不能这样写！！！有直接溢出的风险！！！

    dp[i][j]+=1000000007;
    dp[i][j]%=1000000007;

• **6355. 统计公平数对的数目**【332周赛第二题】

  二分

  还是尽量用lower_bound()和upper_bound()

  • 因为这俩库函数若找不到，返回的是nums.end()，但手写二分找不到的时候只能返回序列中最后一个元素，最后一个元素可能是不符合要求的，但还是会返回

    int l=lower_bound(nums.begin(),nums.end(),lower)-nums.begin();
    int r=upper_bound(nums.begin(),nums.end(),upper)-nums.begin();

  • 如果有不方便使用上述库函数的场景，如需要自己写check()函数，需要手写二分，可以在序列末尾push_back()一个最大的元素，这样可以起到nums.end()的作用

    参考代码

• **6357. 最少得分子序列**【332周赛第四题】

  字符串处理+前后缀分解+查找子串+预处理

  看0x3F的视频题解后自己写的代码（因为粗心写了不少bug，主要还是因为代码逻辑太复杂了）

• **6356. 子字符串异或查询**【332周赛第三题】

  最开始一直TLE，但是仔细看了题目数据范围之后，发现可以将复杂度从n^2^（1e8）优化到（30×30）

  因为有0 <= first_i, second_i <= 10^9，所以结果的范围也是[0, 1e9]，1e9就是（2^10^）^3^，即在二进制字符串表示中只用遍历30bits的长度，所以复杂度可以优化为（30×30）

• 1234. 替换子串得到平衡字符串

  双指针（滑动窗口）

  双指针的难题比较少见，可以多看看

• 1124. 表现良好的最长时间段

  前缀和+哈希

  刚上来想法是双指针，后来发觉不能用

  算是比较反常规的前缀和了（和560很像）

• 1792. 最大平均通过率

  能看出来是用自定义类型的优先队列来做，但是要注意：

  1. 在类内重载运算符的时候，属于类的成员函数，需要隐式地获取第一个参数【参考】

     所以要么在函数声明前面加上friend关键字；要么在类的外面声明这个重载函数

  2. 本题中的类成员用两个int，即int pass, total;

     比用一个vector快多了，因为用vector需要经过多次拷贝复制，会卡时间复杂度

• 1140. 石子游戏 II

  动态规划==回溯+记忆化搜索

  这题多看看罢

• 75. 颜色分类

  基本要求好满足，但是进阶要求一个仅使用常数空间的一趟扫描算法

  双指针（参考）

• 581. 最短无序连续子数组

  要求$$O(n)$$时间求解，要动动脑筋（单调栈可以，但是不知道为啥很慢）

• Trie字典树

  标准写法见我的另一篇文章

  • 208. 实现 Trie (前缀树)

    Trie类中包含两个成员，第一个成员是unordered_map<char, Trie*>，即子节点的值到子节点地址的映射

    第二个成员是子节点的信息，如该节点是否有单词

    class Trie {
        // char c;
        unordered_map<char,Trie *> mp;
        bool flag;
    }

  • 648. 单词替换

    单独写一个Trie类

    类的声明最后要加分号

    Search()方法和Insert()方法可以根据题目适当修改

  • 211. 添加与搜索单词 - 数据结构设计

    unordered_map的Trie树会比直接用数组慢一些

    一定要先count()再取值！map直接取值可能导致本来不存在的键值被添加进去

• 210. 课程表 II

  拓扑排序

• 2. 两数相加

  按位加法

  顺带写了个翻转链表（后面发现误解了题意，本题不需要翻转）

  翻转链表题目链接

• 982. 按位与为零的三元组

  有技巧的枚举 + 常数优化

  将三元组遍历的$$O(n^3)$$复杂度优化到$$O(n^2+C\times n)$$，其中 n 是数组 $$\textit{nums}$$ 的长度，C 是数组 $$\textit{nums}$$ 中的元素范围，在本题中 $$C = 2^{16}$$

• 4. 寻找两个正序数组的中位数

  思路不常见的二分，挺好的题，中心思想是：通过二分，在短的那个数组中找到“分隔线”，复杂度为$O(log\min(m,n)))$

  官方题解的视频讲的很好

• 1096. 花括号展开 II

  用栈计算表达式的题目，比较经典

  与求解中缀表达式一样，在遍历表达式的过程中我们需要用到两个栈，一个用来存放运算符（即加号和乘号，以及左大括号），另一个用来存运算对象（即集合）。

  合并两个set（和求并集不太相同）：std::map<Key,T,Compare,Allocator>::merge

  set1.merge(set2);

• 1590. 使数组和能被 P 整除

  这题是1. 两数之和的plus版

  前缀和+哈希（一时间觉得需要$$O(n^2)$$的复杂度无从下手，就是前缀和+哈希）

• 1616. 分割两个字符串得到回文串

  双指针 还不错的题

• 1073. 负二进制数相加

  模拟加法

  • 与大数加法不同的是，这题需要重新推导进位等值的计算规则，但思路都相同

    如果暴力，会超过long的限制，整数溢出($$2^{1000}$$需要1000位整型来的存储，但long long只有64bits)

  • 以负数为基数的短除法，要确保余数为正，可以在取余后进行判断，如果余数是负，则余数-=基数（基数为负），同时商+=1；或余数+=基数（基数为正），同时商-=1。

  C++vector的截取，使用迭代器的初始化，或assign迭代器

• 1079. 活字印刷

  看了tag才想起来做法

• 1373. 二叉搜索子树的最大键值和

  后序遍历

  能自己写出来，但是效率比较低，不论是写代码的效率还是代码的效率

  经历了两次优化：

  • 第一次：（回溯中需要返回比较多的信息时）新定义了结构体用来传输返回值，同时使得代码可读性提高（不再是vector数组下标来存，而是带有名称的字段）

    C++中定义结构体不需要typedef，只需要

    struct person{
    	string name;
    	int age;
    	bool gender;
    };

    即可。使用时person Donald= {"Trump", 76, ture};

  • 第二次：简化逻辑，减少不必要的分支判断

• LCP 33. 蓄水

  枚举，搞清楚变量之间的关系之后就可以枚举

• 1080. 根到叶路径上的不足节点

  后序遍历

• 2451. 差值数组不同的字符串

  标准库容器支持关系运算符，比较两个 vector 是否相等使用 == 运算符即可。 当两个 vector 包含相同个数的元素，且对位元素都相等时，判定两个 vector 相等，否则不等。

• 1091. 二进制矩阵中的最短路径

  这题我上来第一反应居然是用DFS，这题是BFS最常见的应用：迷宫问题-寻找最短路径

  储存坐标时使用pair<int,int>比使用vector<int>快很多很多

  如果问题需要枚举所有方案，才需要DFS

• 1130. 叶值的最小代价生成树

  标准的区间dp，复杂度为$$O(n^3)$$

  注意不要漏掉“数组 arr 中的值与树的中序遍历中每个叶节点的值一一对应”的条件

• ==53. 最大子数组和==

  动态规划：时间复杂度$O(n)$，空间复杂度$O(1)$

  1186. 删除一次得到子数组最大和

  • 动态规划：时间复杂度$O(n)$，空间复杂度$O(n)$【我的方法：两边延伸最大子数组和】

  • 动态规划：时间复杂度$O(n)$，空间复杂度$O(1)$【官解方法：一遍遍历+$O(1)$空间（分是否删除过的两种情况进行讨论）】

• 215. 数组中的第K个最大元素

  基于快速排序的选择方法

  ==快速排序都不会写啦？？==快速排序笔记详见这里

  void quick_sort(int q[], int l, int r)
  {
      if (l >= r) return;
  
      int i = l - 1, j = r + 1, x = q[l + r >> 1];
      while (i < j)
      {
          do i ++ ; while (q[i] < x);
          do j -- ; while (q[j] > x);
          if (i < j) swap(q[i], q[j]);
      }
      quick_sort(q, l, j), quick_sort(q, j + 1, r);
  }

• 1911. 最大子序列交替和

  代码很短的动态规划，但是一是想不到可以用动态规划，二是想不出转移方程

• 239. 滑动窗口最大值

  模拟——单调队列

• 979. 在二叉树中分配硬币

  dfs递归，思路不好想，代码不难

• 834. 树中距离之和

  dfs递归，换根 DP，思路不好想

• 1851. 包含每个查询的最小区间

  （好题）离线算法+优先队列

  在线算法和离线算法参见这里的评论区

• 874. 模拟行走机器人

  模拟+哈希。把二维坐标哈希成一维存储在set里

  二维的寻路+障碍

• 918. 环形子数组的最大和

  《子数组的最大和》的变体，需要将非环形和环形分开讨论

• **2681. 英雄的力量**——2060

  dp+前缀和（2060分数比较合适，方法都会但是想不到）

• 21. 合并两个有序链表

  递归，没那么好想到；但想到之后非常简单

  24. 两两交换链表中的节点

  该题递归的解法跟上题相似

• 1444. 切披萨的方案数

  二维前缀和+三维dp

• 本文作者：wan_nan
• 本文链接：https://wan-nan.github.io/2022/10/29/LEETCODE-TOP100/
• 版权声明：本博客所有文章除特别声明外，均默认采用 许可协议。